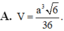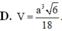Do S.ABCD là chóp đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà BD là giao tuyến (MBD) và (ABCD)
\(\Rightarrow\widehat{MOC}\) là góc giữa (MBD) và (ABCD)
\(OC=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\) ; \(MC=OM=\dfrac{1}{2}SC=\dfrac{a}{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{MOC}=\dfrac{OM^2+OC^2-CM^2}{2OM.OC}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MOC}=45^0\)