Đáp án A
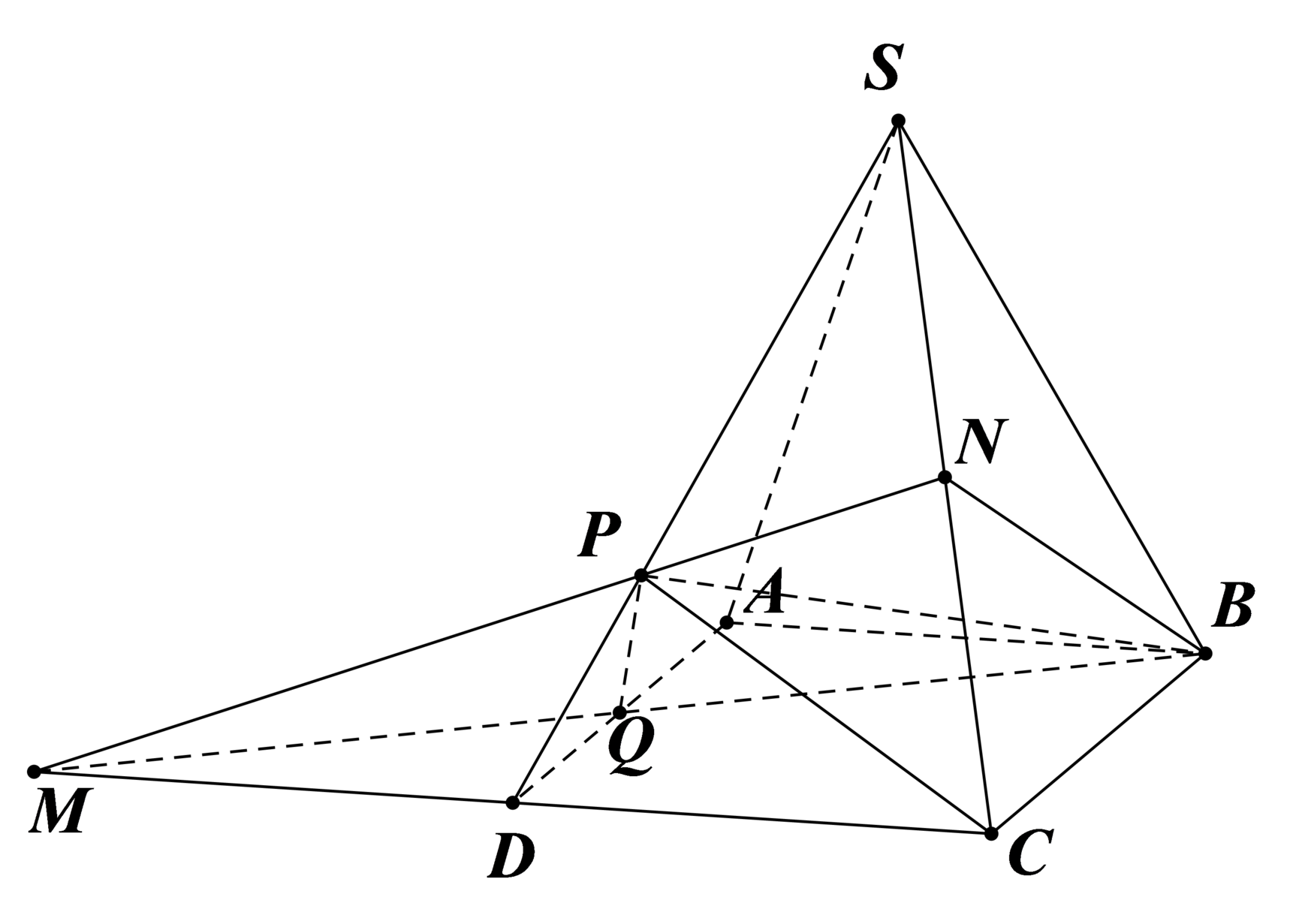
Áp dụng định lí Menelaus cho Δ S C D ta có:
N S N C . M C M D . P D P S = 1 ⇒ P D P S = 1 2 ⇒ P D S D = 1 3 .
Ta có: V P . B Q D C V S . A B C D = 1 3 . d P , A B C D . S B C D Q 1 3 . d S , A B C D . S A B C D = 1 3 . 3 4 = 1 4
⇒ V P . B Q D C = 1 4 V S . A B C D .
V P . N C B V S . A B C D = V P . N C B 2. V D . S C B = 1 3 . d P , S C B . S Δ N C B 2. 1 3 . d D , S C B . S Δ S C B = 1 2 . 2 3 . 1 2 = 1 6 ⇒ V P . N C B = 1 6 V S . A B C D .
Do đó V P Q D . N B C = V P . B Q D C + V P . N C B = 5 12 V S . A B C D .
Vậy tỉ số thể tích của 2 phần cần tìm là 7 5 .