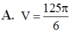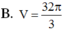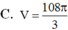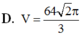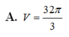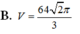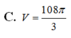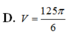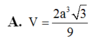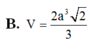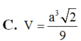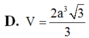Do \(SA=SB=SC=SD\) và đáy là hình vuông nên \(SABCD\) là chóp đều
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Theo tính đối xứng của chóp đều \(\Rightarrow SB'=SD'\Rightarrow B'D'||BD\)
Gọi M là giao điểm SO và AC' \(\Rightarrow M\in B'D'\) (t/c giao tuyến 3 mp cắt nhau)
Áp dụng định lý Talet:
\(\dfrac{SM}{SO}=\dfrac{SD'}{SD}=\dfrac{SB'}{SB}=\dfrac{2}{3}\Rightarrow M\) là trọng tâm tam giác SAC
\(\Rightarrow C'\) là trung điểm SC \(\Rightarrow\dfrac{SC'}{SC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{V_{SAB'C'D'}}{V_{SABCD}}=\dfrac{2V_{SAB'C'}}{2V_{SABC}}=\dfrac{V_{SAB'C'}}{V_{SABC}}=\dfrac{SA}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=1.\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\)