Đáp án C.
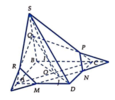
Trong (ABCD) gọi
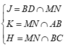
Trong (SBC) gọi: ![]()
Trong (SBD) gọi: Q = IJ ∩ SB
Trong (SBC) gọi: R = KQ ∩ SA
Suy ra, thiết diện là ngũ giác MNPQR.
Đáp án C.

Trong (ABCD) gọi
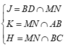
Trong (SBC) gọi: ![]()
Trong (SBD) gọi: Q = IJ ∩ SB
Trong (SBC) gọi: R = KQ ∩ SA
Suy ra, thiết diện là ngũ giác MNPQR.
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M,N,I lần lượt là trung điểm của AD,CD,SO. Tìm thiết diện của hình chóp S.ABCD với mặt phẳng (MNI)
Cho chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là trung điểm AD, CD; I là điểm trên SO. Tìm thiết diện hình chóp với mặt phẳng (MNI) Mng kẻ hình và giải chi tiết giúp e với ạ, e cảm ơn
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì
A. AB = 3CD
B. AB = 2CD
C. CD = 3AB
D. CD = 2AB
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp ![]() cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?
cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?

A. AB=3CD
B. AB=2CD
C. CD=2AB
D. CD=3AB
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm của CD, CB, SA Thiết diện của hình chóp cắt bởi mặt phẳng (MNK) là một đa giác (H). Hãy chọn khẳng định đúng.
A. (H)là một hình thang.
B. (H) là một ngũ giác
C. (H) là một hình bình hành.
D.(H) là một tam giác.
Cho hình chóp S.ABCD đáy ABCD là hình bình hành, tâm O. K là trung đểm của SA. Xác định vị trí của H trên AC để thiết diện của hình chóp S.ABCD với mặt phẳng (∝) chứa KH và song song với BD là ngũ giác.
A. H thuộc đoạn OC và khác O, C
B. H thuộc đoạn OA và khác O, A
C. H thuộc đoạn AC và khác A, C
D. H thuộc đoạn AC và khác A, C
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (GIJ) với hình chóp S.ABCD là hình bình hành.
A. AB = CD
B. AB = 3CD
C. 3AB = CD
D. AB = 2CD
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với AI = x (0 < 0 < a). Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).
a) Xác định thiết diện của mặt phẳng với hình chóp S.ABCD.
b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.