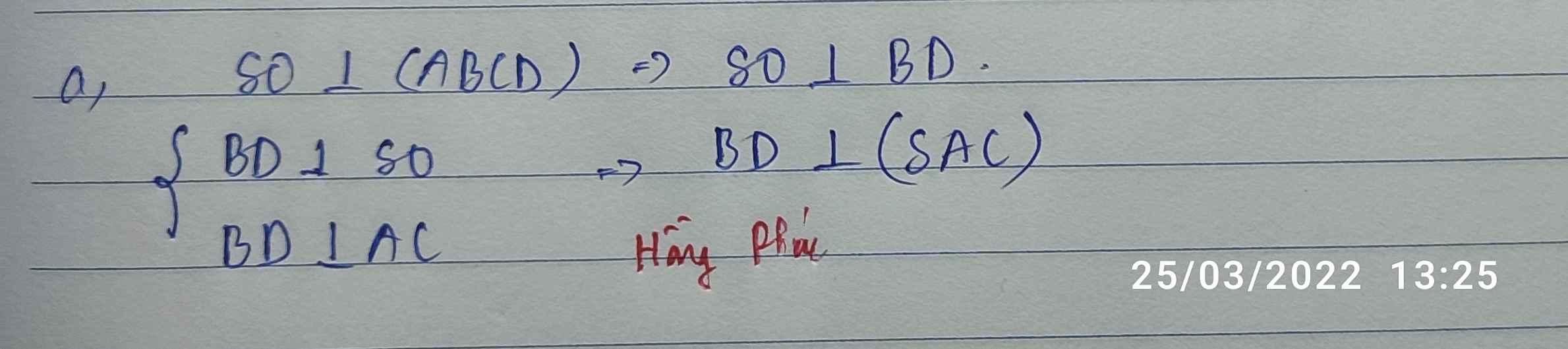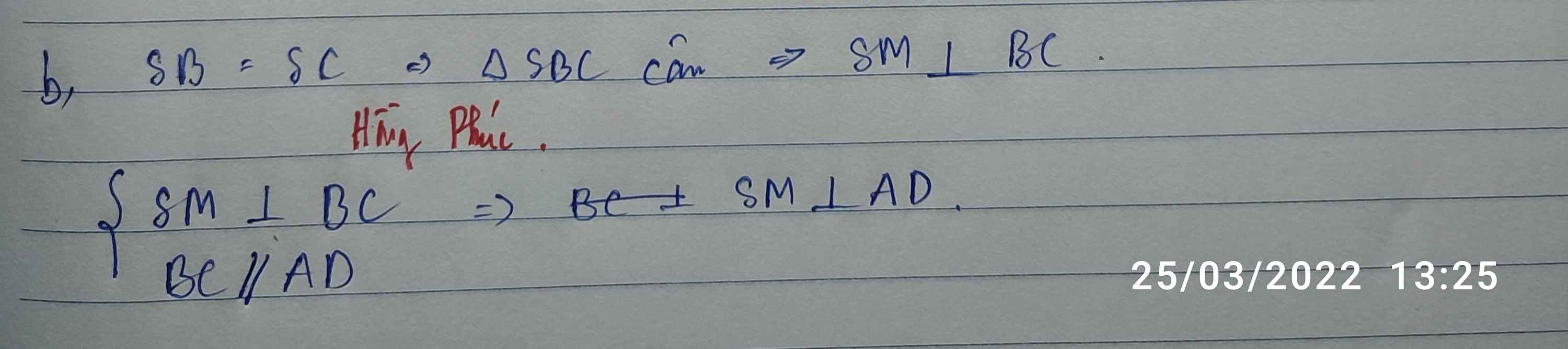Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, BC = a√3 và SA vuông góc (ABCD). Góc giữa SC và mặt phẳng (ABCD) bằng 45°. Gọi M là trung điểm của đoạn OA. Chứng minh (SAC) vuông góc (SBM)
cho hình chóp S.ABCD với đáy là hình chữ nhật,AD=2a,AB=a; O là giao điểm của AC và BD, SO vuông góc với mặt phẳng (ABCD) và SO=a/2. Gọi M là trung điểm của BC.
a)Chứng minh SM vuông góc mặt phẳng (SAD)
b) Gọi \(\phi\) là góc giữa đường thẳng SC và mặt phẳng (SAD), tính sin\(\phi\)
Cho hình chóp S ABCD . có đáy ABCD là hình vuông tâm O , cạnh bằng, 2a . SA vuông góc với mặt đáy và SA =a .
a) Chứng minh: BD vg (SAC) .
b) Gọi N là trung điểm của CD . Xác định và tính góc giữa đường thẳng SN với mặt phẳng (SBD).
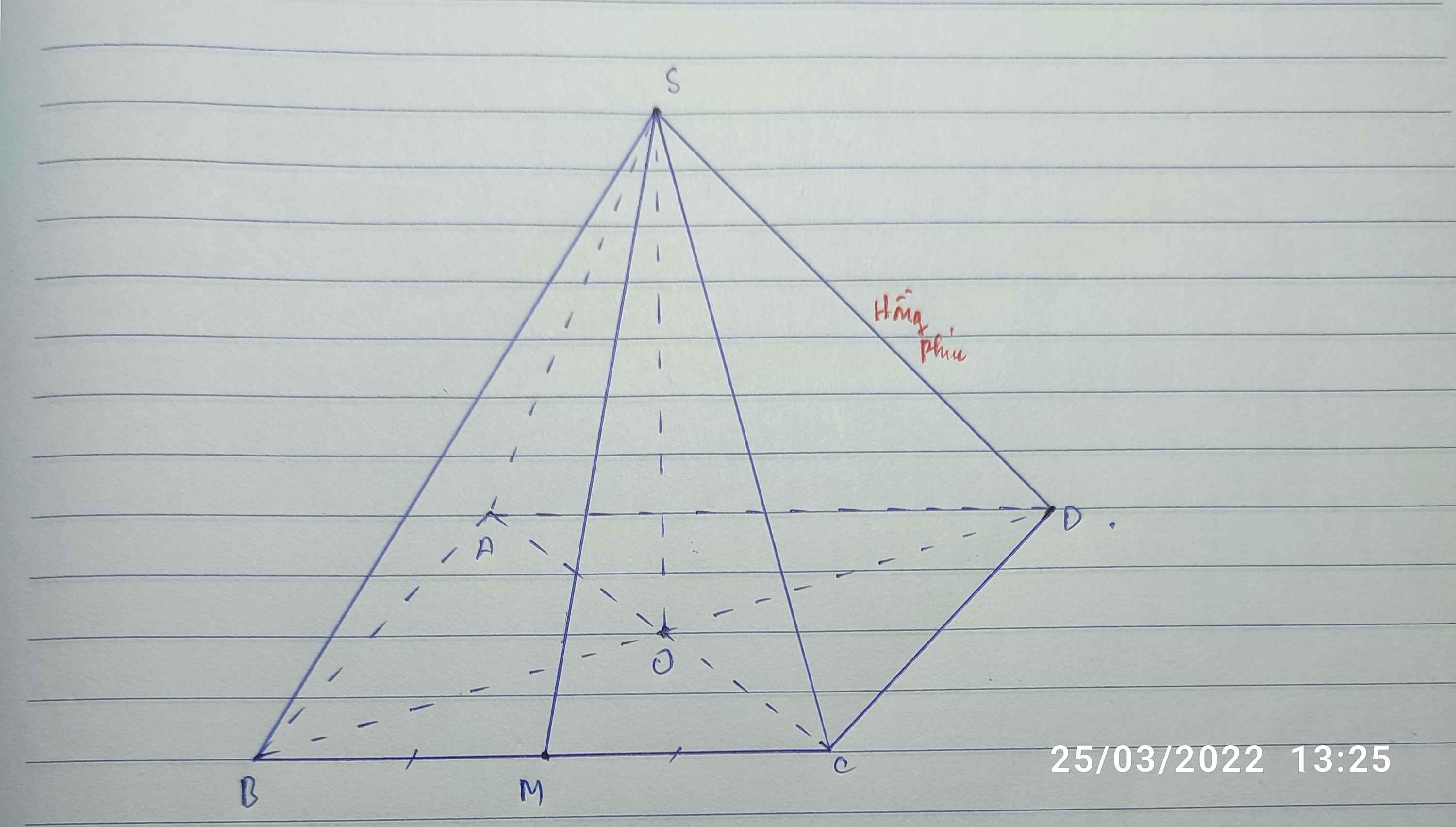
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
Cho hình chóp S.ABCD có đáy là hình vuông tâm O , cạnh a ; các cạnh bên của hình chóp cùng bằng a. Chứng minh rằng đường thẳng BD vuông góc với (SAC)b. Gọi P là mặt phẳng đi qua A và vuông góc với đường thẳng SC. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (P)c. Tính góc giữa mặt phẳng (P) và đường thẳng AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông tâm O , cạnh a ; các cạnh bên của hình chóp cùng bằng
a. Chứng minh rằng đường thẳng BD vuông góc với (SAC)
b. Gọi P là mặt phẳng đi qua A và vuông góc với đường thẳng SC. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (P)
c. Tính góc giữa mặt phẳng (P) và đường thẳng AB
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông (ABC) SA= a cân 3; AB=a
A: Chứng minh (SAB) vuông (SAC)
B: Gọi M là trung điểm của BC, chứng minh BC vuông góc vs SM
C: Tính góc giữa SC và (ABC
cho hình chóp s.ABCD đáy ABCD là hình vuông tâm o cạnh a SA vuông góc ABCD SA = a√3 a chứng minh BD vuông góc sac b khoảng cách từ b đến SAB
Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SB = SC = SD. Chứng minh rằng:
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phẳng (SAC).
Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc
B
A
D
60
o
. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO 3a/4 . Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).
Đọc tiếp
Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc B A D = 60 o . Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO = 3a/4 . Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).
b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).