Các câu hỏi tương tự
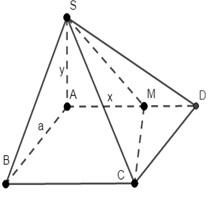
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh SA vuông góc với đáy và SA y. Trên cạnh AD lấy điểm M sao cho
A
M
x
. Biết rằng
x
2
+
y
2
a
2
.
Tìm giá trị lớn nhất của thể tích khối chóp S.ABCM A.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh SA vuông góc với đáy và SA= y. Trên cạnh AD lấy điểm M sao cho A M = x . Biết rằng x 2 + y 2 = a 2 . Tìm giá trị lớn nhất của thể tích khối chóp S.ABCM
A. a 3 3 4
B. a 3 8
C. a 3 3 2
D. a 3 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA y 0 và vuông góc với đáy. Trên AD lấy điểm M, đặt AM x (0 x a) . Nếu
x
2
+
y
2
a
2
thì giá trị lớn nhất của thể tích S.ABCM bằng: A.
a
3
3
3
B.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = y > 0 và vuông góc với đáy. Trên AD lấy điểm M, đặt AM = x (0 < x < a) . Nếu x 2 + y 2 = a 2 thì giá trị lớn nhất của thể tích S.ABCM bằng:
A. a 3 3 3
B. a 3 3 8
C. a 3 3 24
D. 3 a 3 3 8
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A, B, D). sao cho
A
B
A
M
+
2.
A
D
A
N
4.
Kí hiệu V,
V
1
lần lượt là thể tích của các khối chóp...
Đọc tiếp
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A, B, D). sao cho A B A M + 2. A D A N = 4. Kí hiệu V, V 1 lần lượt là thể tích của các khối chóp S . A B C D v à S . M B C D N . Tìm giá trị lớn nhất của V 1 V
A. 2 3
B. 3 4
C. 1 6
D. 14 17
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,
S
A
⊥
A
B
C
D
biết
S
A
y
;
M
∈
A
D
;
A
M
x
;
x
2
+
y
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ A B C D
biết S A = y ; M ∈ A D ; A M = x ; x 2 + y 2 = a 2
. Khi đó V S . A B C M m a x là
A. a 3 3 4
B. a 3 8
C. a 3 3 2
D. a 3 3 8
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0xa). Mặt phẳng
(
α
)
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.
x
a
4
B.
x
a
3
C.
x
a...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0<x<a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hàm số
f
x
a
x
+
b
c
x
+
d
với
a
,
b
,
c
,
d
∈
R
có đồ thị hàm số yf(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số yf(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng. A. 2 B. 5 C. 4...
Đọc tiếp
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x
0
x
α
. Mặt phẳng
α
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.
x
a
4
B.
x...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x 0 < x < α . Mặt phẳng α qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp S.ABCD có đáy là hình thang cân,
S
A
⊥
A
B
C
D
,
A
D
2
B
C
2
A
B
. Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông? A. 3 B. 6 C. 5 D. 7
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Trong không gian Oxyz cho đường thẳng d:
x
2
y
2
z
+
3
-
1
và mặt cầu (S):
(
x
-
3
)
2
+
(
y
-
2
)
2
+
(
z
-...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng d: x 2 = y 2 = z + 3 - 1 và mặt cầu (S): ( x - 3 ) 2 + ( y - 2 ) 2 + ( z - 5 ) 2 = 36 . Gọi Δ là đường thẳng đi qua A(2;1;3) vuông góc với đường thẳng (d) và cắt (S) tại 2 điểm có khoảng cách lớn nhất. Khi đó đường thẳng Δ có một vectơ chỉ phương là u → ( 1 ; a ; b ) . Tính a + b
A. 4
B. -2
C. - 1 2
D. 5