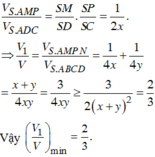Các câu hỏi tương tự
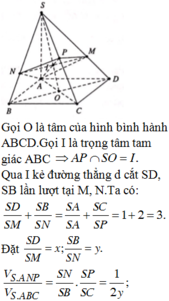
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi
V
1
là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của
V
1
V
?
A.
1
8
B.
2
3
C.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi V 1 là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của V 1 V ?
A. 1 8
B. 2 3
C. 3 8
D. 1 3
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi
V
1
là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của
V
1
V
? A.
1
8
B.
2
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi V 1 là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của V 1 V ?
A. 1 8
B. 2 3
C. 3 8
D. 1 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi
V
1
là thể tích khối chóp S.AMPN. Giá trị lớn nhất của
V
1
V
thuộc khoảng nào sau đây? A.
0
;
1
5...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi V 1 là thể tích khối chóp S.AMPN. Giá trị lớn nhất của V 1 V thuộc khoảng nào sau đây?
A. 0 ; 1 5 .
B. 1 5 ; 1 3 .
C. 1 3 ; 1 2 .
D. 1 2 ; 1 .
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi
V
1
là thể tích của khối chóp S.AMPQ. Tìm giá trị nhỏ nhất của
V
1
V
. A. 1/8 B. 2/3 C. 8/3 D. 1/3
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi V 1 là thể tích của khối chóp S.AMPQ. Tìm giá trị nhỏ nhất của V 1 V .
A. 1/8
B. 2/3
C. 8/3
D. 1/3
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SB và SD lần lượt tại M và N. Gọi V1 là thể tích của khối chóp S.AMP. Giá trị nhỏ nhất của tỉ số bằng
V
1
V
A. 1/3 B. 1/8 C. 2/3 D. 3/8
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng V. Điểm P là trung điểm của SC, một mặt phẳng qua AP cắt hai cạnh SB và SD lần lượt tại M và N. Gọi V1 là thể tích của khối chóp S.AMP. Giá trị nhỏ nhất của tỉ số bằng V 1 V
A. 1/3
B. 1/8
C. 2/3
D. 3/8
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm của SC. Mặt phẳng qua AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi
V
1
, V thứ tự là thể tích của khối chóp S.AMKN và khối chóp S.ABCD. Giá trị nhỏ nhất của tỷ số
V
1
V
bằng A. 1/3 B. 3/8 C. 1/2 D. 2/3
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm của SC. Mặt phẳng qua AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi V 1 , V thứ tự là thể tích của khối chóp S.AMKN và khối chóp S.ABCD. Giá trị nhỏ nhất của tỷ số V 1 V bằng
A. 1/3
B. 3/8
C. 1/2
D. 2/3
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số
V
V
có giá trị nhỏ nhất bằng A.
1
5
.
B.
3
8
.
C.
1
3
.
D.
1...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số V ' V có giá trị nhỏ nhất bằng
A. 1 5 .
B. 3 8 .
C. 1 3 .
D. 1 2 .
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi
V
1
, V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số
V
1
V
bằng: A.
1
2
B.
2
3
C.
1...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi V 1 , V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số V 1 V bằng:
A. 1 2
B. 2 3
C. 1 3
D. 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I nằm trên cạnh SC sao cho IS 2IC. Mặt phẳng (P) chứa cạnh AI cắt cạnh SB, SD lần lượt tại M, N. Gọi
V
’
,
V
lần lượt là thể tích khối chóp S.AMIN và S.ABCD. Tính giá trị nhỏ nhất của tỷ số thể tích
V
V
A.
4
5
B.
5
54
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I nằm trên cạnh SC sao cho IS = 2IC. Mặt phẳng (P) chứa cạnh AI cắt cạnh SB, SD lần lượt tại M, N. Gọi V ’ , V lần lượt là thể tích khối chóp S.AMIN và S.ABCD. Tính giá trị nhỏ nhất của tỷ số thể tích V ' V
A. 4 5
B. 5 54
C. 8 15
D. 5 24