Đáp án B
Phương pháp:
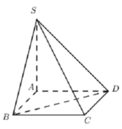
Suy luận từng đáp án, sử dụng phương pháp chứng minh đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng đó.

Đáp án B

Phương pháp:
Suy luận từng đáp án, sử dụng phương pháp chứng minh đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng đó.

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và S A = 3 a . Chọn hệ trục tọa độ Oxyz sao cho A trung với O, điểm B thuộc tia Ox, điểm D thuộc tia Oy và điểm S thuộc tia Oz. Gọi G là trọng tâm của tam giác SBD. Mệnh đề nào dưới đây là đúng?
A. G a 2 ; a 2 ; 3 a 2
B. G a 3 ; a ; a 3
C. G(a;a;3a)
D. G a 3 ; a 3 ; a
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA=3a. Chọn hệ trục tọa độ Oxyz sao cho A trùng với O, điểm B thuộc tia Ox, điểm D thuộc tia Oy và điểm S thuộc tia Oz. Gọi G là trọng tâm của tam giác SBD. Mệnh đề nào dưới đây là đúng?
A. G a 3 ; a 3 ; a
B. G a ; a ; 3 a
C. G a 2 ; a 2 ; 3 a 2
D. G a 3 ; a ; a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA=3a. Chọn hệ trục tọa độ Oxyz sao cho A trùng với O, điểm B thuộc tia Ox, điểm D thuộc tia Oy và điểm S thuộc tia Oz. Gọi G là trọng tâm của tam giác SBD. Mệnh đề nào dưới dây là đúng?
A. G a 2 ; a 2 ; 3 a 2
B. G a 3 ; a ; a 2
C. G a ; a ; 3 a
D. G a 3 ; a 3 ; a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S có SA=SB=2a nằm trong mặt phẳng vuông góc với đáy ABCD. Gọi α là góc giữa SD và mặt phẳng đáy (ABCD). Mệnh đề nào sau đây đúng
A. tan α = 3
B. c o t α = 3 6
C. tan α = 3 3
D. c o t α = 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S có S A = S B = 2 a nằm trong mặt phẳng vuông góc với đáy ABCD. Gọi α là góc giữa SD và mặt phẳng đáy (ABCD). Mệnh đề nào sau đây đúng?
A. tan α = 3
B. c o t α = 3 6
C. tan α = 3 3
D. c o t α = 2 3
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy S A = a 2 . Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên đáy ABCD trùng với trung điểm AB. Biết A B = a , B C = 2 a , B D = a 10 . Góc giữa hai mặt phẳng (SBD) và đáy là 60 ° . Tính d là khoảng cách từ A đến mặt phẳng (SCD) gần với giá trị nào nhất trong các giá trị sau đây ?
A. 0,80a
B. 0,85a
C. 0,95a
D. 0,98a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với đáy. Mệnh đề nào sau đây sai?
A. C D ⊥ S A D .
B. B D ⊥ S A C .
C. B C ⊥ S A B .
D. A C ⊥ S B D .