Question

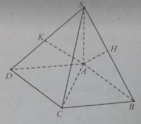
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Cho hình SA vuông góc với ABCD . Gọi h, i, k lần lượt là hình chiếu của A trên SB, SC, SD. CMR

a, BC nguồn gốc với SAB, CD vuông góc với SAD, AC vuông góc với SBD.

b, AH vuông góc với SC, AK vuông góc với SC và từ đó suy ra AH, AK đồng phẳng.

c. Tứ giác AH IK có hai đường chéo vuông góc.

Answer 1

a: Ta có: BC\(\perp\)AB

BC\(\perp\)SA(SA\(\perp\)(ABCD))

AB,SA cùng thuộc mp(SAB)

Do đó: BC\(\perp\)(SAB)

CD\(\perp\)AD

CD\(\perp\)SA(SA\(\perp\)(ABCD))

SA,AD cùng thuộc mp(SAD)

Do đó: CD\(\perp\)(SAD)

Ta có: BD\(\perp\)AC

BD\(\perp\)SA(SA\(\perp\)(ABCD))

AC,SA cùng thuộc mp(SAC)

Do đó: BD\(\perp\)(SAC)

b: BC\(\perp\)(SAB)

mà AH thuộc mp(SAB)

nên BC\(\perp\)AH

mà AH\(\perp\)SB

và BC,SB cùng thuộc mp(SBC)

nên AH\(\perp\)(SBC)

=>AH\(\perp\)SC(2)

CD\(\perp\)(SAD)

=>CD\(\perp\)AK

mà AK\(\perp\)SD
và CD,SD cùng thuộc mp(SCD)

nên AK\(\perp\)(SCD)

=>AK\(\perp\)SC(1)

Từ (1),(2) suy ra AH,AK đồng phẳng