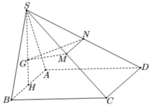
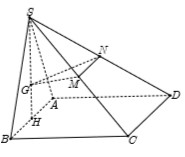
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = 2 , A D = 2 3 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD) . Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD).
A. 2 435 145
B. 11 145 145
C. 2 870 145
D. 3 145 145
Đáp án B
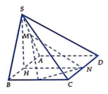
Gọi H là trung điểm của cạnh AB. Khi đó S H ⊥ ( A B C D )
Ta có S H ⊥ A B ; A B ⊥ H N ; H N ⊥ S H và S H = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó:
B ( 1 ; 0 ; 0 ) ; A ( - 1 ; 0 ; 0 ) ; N ( 0 ; 2 3 ; 0 ) ; C ( 1 ; 2 3 ; 0 ) ; D ( - 1 ; 2 3 ; 0 ) ; S ( 0 ; 0 ; 3 ) ; M ( - 1 2 ; 0 ; 3 2 ) ; P ( 1 ; 3 ; 0 )
Mặt phẳng (SCD) nhận n 1 → = - 3 6 C D → , S C → = 0 ; 1 ; 2 làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận n 2 → = - 2 3 3 M N → , M P → = 3 ; 1 ; 5 làm một vectơ pháp tuyến.
Gọi ∅ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
cos ∅ = n 1 → . n 2 → n 1 → . n 2 → = 11 145 145