Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I nằm trên cạnh SC sao cho I S = 2 I C . Mặt phẳng (P)chứa cạnh AI cắt cạnh SB;SD lần lượt tại M;N. Gọi V ' , V lần lượt là thể tích khối chóp S . A M I N và S . A B C D . Tính giá trị nhỏ nhất của tỷ số thể tích V V '
A. 4/5
B. 5/54
C. 8/15
D. 5/24
Đáp án C
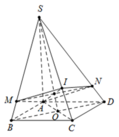
Gọi O là tâm của hình bình hành ABCD
Gọi H = S K ∩ A I qua H kẻ d / / B D cắt SB;SD lần lượt tại M;N
Xét tam giác SAC có
I S I C . A C O C . O H S H = 1 ⇒ O H S C = 1 4 ⇒ S H S C = 4 5
Mà M N / / B D → S M S B = S N S D = S H S O = 4 5
Ta có V S . A M I V S . A C D = S M S B . S I S C = 2 3 . S M S B ⇒ V S . A M I V S . A B C D = 1 3 . S M S B
Và V S . A N I V S . A C D = S N S D . S I S C = 2 3 . S D S D ⇒ V S . A N I V S . A B C D = 1 3 . S N S D
Suy ra V ' V = 1 3 S M S B + S N S D = 1 3 . 4 5 + 4 5 = 8 15



