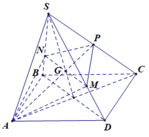
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, O lần lượt là trung điểm của AB, CD và AC. Chứng minh rằng
a) \(\overrightarrow{BN}+\overrightarrow{DM}\) đối nhau
b) \(\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{4SO}\)
c) \(\overrightarrow{SD}-\overrightarrow{BN}-\overrightarrow{CM}=\overrightarrow{SC}\)
a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(DN=NC=\dfrac{DC}{2}\)
mà AB=DC(ABCD là hình bình hành)
nên AM=MB=DN=NC
Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
=>\(\overrightarrow{BN};\overrightarrow{DM}\) là hai vecto đối nhau
b: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của BD
Xét ΔSBD có SO là đường trung tuyến
nên \(\overrightarrow{SB}+\overrightarrow{SD}=2\cdot\overrightarrow{SO}\)
Xét ΔSAC có SO là đường trung tuyến
nên \(\overrightarrow{SA}+\overrightarrow{SC}=2\cdot\overrightarrow{SO}\)
\(\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=2\cdot\overrightarrow{SO}+2\cdot\overrightarrow{SO}=4\cdot\overrightarrow{SO}\)
c: \(\overrightarrow{SD}-\overrightarrow{BN}-\overrightarrow{CM}=\overrightarrow{SD}-\overrightarrow{MD}+\overrightarrow{MC}\)
\(=\overrightarrow{SD}+\overrightarrow{DM}+\overrightarrow{MC}=\overrightarrow{SD}+\overrightarrow{DC}=\overrightarrow{SC}\)