Chọn D
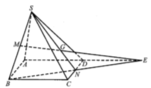
Gọi N là trung điểm của CD, khi đó MG, BN, AD đồng quy tại E.
Do AB = 2ND nên ND là đường trung bình của tam giác EAB ⇒ D là trung điểm của AE
Chọn D

Gọi N là trung điểm của CD, khi đó MG, BN, AD đồng quy tại E.
Do AB = 2ND nên ND là đường trung bình của tam giác EAB ⇒ D là trung điểm của AE
Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh SA; các điểm E,F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh SB,SD lần lượt tại các điểm N,P. Thể tích của khối đa diện ABCDMNP bằng
A. 2 3
B. 1 3
C. 3 4
D. 1 4
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB. SC và P là điểm trên cạnh SD sao cho S P S D = 3 4 . Mặt phẳng (MNP) cắt cạnh SB tại điểm Q. Tỉ số S Q S B bằng
A. 3 4
B. 2 3
C. 2 5
D. 4 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và A B C = 60 ° . Hình chiếu vuông góc của điểm S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABC. Gọi φ là goc giữa đường thẳng SB và mặt phẳng (SCD), tính sin φ biết rằng SB = a.
A. sin φ = 1 4
B. sin φ = 1 2
C. sin φ = 3 2
D. sin φ = 2 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và A B C ^ = 60 ° . Hình chiếu vuông góc của điểm S lên mặt phẳng A B C D trùng với trọng tâm tam giác ABC. Gọi φ là góc giữa đường thẳng SB với mặt phẳng S C D , tính sin φ biết rằng S B = a .
A. sin φ = 2 2
B. sin φ = 2 3
C. sin φ = 3 2
D. sin φ = 6 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang AB//CD. Gọi I, J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB. Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng?
A. AB=3CD
B. A B = 1 3 C D
C. A B = 3 2 C D
D. A B = 2 3 C D
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác ABC và M là trung điểm SC. Gọi K là giao điểm của SD với mặt phẳng (AGM). Tính tỉ số K S K D
A. 1/2
B. 1/3
C. 2
D. 3
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF.
A. V = a 3 6 36 .
B. V = a 3 6 9 .
C. V = a 3 6 6 .
D. V = a 3 6 18 .
Cho hình chóp S.ABCD có đáy là hình thang. AD//BC, AD=2BC=2a. Gọi E, F lần lượt là trọng tâm các tam giác SAD và SBC. Gọi d là giao tuyến của hai mặt phẳng (EBC) và (FAD); M,N lần lượt là giao điểm của d với các mặt phẳng (SAB), (SCD). Độ dài đoạn thẳng MN bằng
A. 6 a 5
B. 3 a 2
C. 2 a 3
D. 5 a 6
Cho hình chóp tứ giác S . A B C D đáy là hình bình hành có thể tích bằng V. Lấy điểm B’, D’ lần lượt là trung điểm của cạnh SB và SD. Mặt phẳng qua A B ' D ' cắt cạnh SC tại C’. Khi đó thể tích khối chóp S . A B ' C ' D ' bằng
A. V 3
B. 2 V 3
C. V 3 3
D. V 6