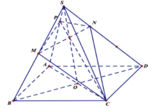
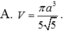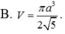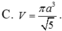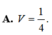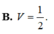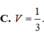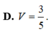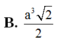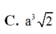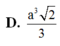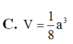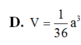Xét ΔSAB có \(\frac{SE}{SA}=\frac{SF}{SB}\left(=\frac13\right)\)
nên EF//AB
Xét ΔSAB có EF//AB
nên \(\frac{EF}{AB}=\frac{SF}{SB}=\frac13\)
=>\(\overrightarrow{EF}=\frac13\cdot\overrightarrow{AB}\)
mà \(\overrightarrow{AB}=\overrightarrow{DC}\) (ABCD là hình bình hành)
nên \(\overrightarrow{EF}=\frac13\cdot\overrightarrow{DC}\)