Đáp án A
Ta có SC là đường kính của mặt cầu ngoại tiếp hình chóp S.ABCD vì các góc ở đỉnh A, B, D đều nhìn SC dưới góc 90 độ

Đáp án A
Ta có SC là đường kính của mặt cầu ngoại tiếp hình chóp S.ABCD vì các góc ở đỉnh A, B, D đều nhìn SC dưới góc 90 độ

Cho hình chóp S.ABCD có A B C ⏜ = A D C ⏜ = 90 ∘ , cạnh bên SA vuông góc với mặt phẳng (ABCD), góc tạo bởi SC và mặt phẳng đáy bằng 60 ∘ , C D = a và tam giác ADC có diện tích bằng a 2 3 2 . Diện tích mặt cầu S m c ngoại tiếp hình chóp S.ABCD là
A. S m c = 16 π a 2
B. S m c = 4 π a 2
C. S m c = 32 π a 2
D. S m c = 8 π a 2
Cho hình chóp S.ABCD có A B C ^ = A D C ^ = 90 ° . Cạnh bên SA vuông góc với mặt phẳng A B C D , góc tạo bởi SC và mặt phẳng đáy bằng 60°, C D = a và Δ A D C có diện tích bằng a 2 3 2 . Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD là
A. S = 16 π a 2
B. S = 4 π a 2
C. S = 32 π a 2
D. S = 8 π a 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng
A. πa 3 3
B. 2 πa 3 3
C. πa 3 6
D. 11 11 πa 3 162
Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SD = a 3 , SC tạo với mặt phẳng đáy (ABCD) một góc Thể tích khối chóp S.ABCD theo a là
A. 4 a 3 3 .
B. 3 a 3 10 .
C. 4 a 3 15 5 .
D. 2 a 3 15 3 .
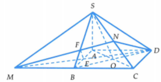
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , B A D ⏜ = 60 0 và SA vuông góc với mặt phẳng A B C D . Góc giữa hai mặt phẳng S B D và A B C D bằng 45 0 . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng M N D chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 và khối đa diện còn lại có thể tích bằng V 2 . Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
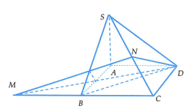
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên đây). Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a 3 , A D = a , S A vuông góc với mặt phẳng đáy và mặt phẳng (SBC) tạo với mặt đáy một góc 60 ° . Tính thể tích V của khối cầu ngoại tiếp khối chóp S. ABCD.
A. V = 13 13 π a 3 6
B. V = 5 10 π a 3 3
C. V = 13 13 π a 3 24
D. V = 5 10 π a 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , AD = 2a .Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Đường thẳng SC tạo với đáy một góc 60 ° Khi đó, thể tích của khối chóp S.ABCD bằng
A. a 3 17 3
B. a 3 17 3
C. a 3 17 9
D. a 3 17 6