Chọn C
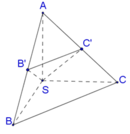
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC
Ta có
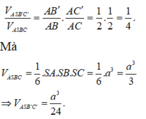
Chọn C

Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC
Ta có
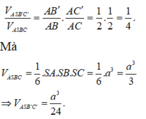
Cho hình chóp S.ABC có SA vuông góc với (ABC), AB=a, AC=a 2 , B A C ^ = 45 ° . Gọi B',C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A.BCC'B'.
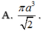
![]()
![]()
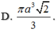
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.

A. k = 1 3
B. k = 2 4
C. k = 4 9
D. k = 2 3
cho hình chóp SABC có SA vuông góc với đáy. Gọi thể tích của SABC=V.
1)Gọi M là hình chiếu của A lên SB a)VSAMC=1/2V b)VSAMC=1/3V c)VSAMC=(SA/SB)².V
2)Gọi M,N lần lượt là hình chiếu của A lên SB,SC
A)VSAMN=1/4V
B)VSAMN=1/9V
C)VSAMN=(SA/SB)².(SA/SC)²
Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt phẳng qua A vuông góc với SC cắt SB, SC lần lượt tại M, N. Biết rằng SA = AC = 5, AB = 3, BC = 4. Thể tích khối chóp S.AMN bằng:
A. 125 68 B. 125 34
C. 175 34 D. 125 17
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.
A. V = 14 54 a 3
B. V = 14 64 a 3
C. V = 14 49 a 3
D. V = 4 61 a 3
Cho hình chóp S . A B C có S A = a ; A B = a 3 ; B A C ^ = 150 o và S A vuông góc với mặt phẳng đáy. Gọi M , N lần lượt là hình chiếu vuông góc của A trên SB và SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C M N bằng.
A. 4 7 π a 3 3
B. 44 11 π a 3 3
C. 28 7 π a 3 3
D. 20 5 π a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Gọi B’, D’ là hình chiếu của A lần lượt trên SB, SD. Mặt phẳng (AB’D’) cắt SC tại C’. Thể tích khối chóp S.AB’C’D’ là
A. V = 2 a 3 3 3
B. V = 2 a 3 2 3
C. V = 2 a 3 3 9
D. V = a 3 3 9
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
Cho hình chóp S.ABC có SA vuông góc với (ABC), A B = a ; A C = a 2 ; B A C ^ = 45 o .Gọi B 1 ; C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C C 1 B 1 bằng
A. πa 3 2
B. πa 3 2
C. 4 3 πa 3
D. πa 3 2 3