Đáp án C
* Hướng dẫn giải:
Hình chop S.ABC thoả mãn SA = SB = SC do đó S thuộc trục đường tròn ngoại tiếp tam giác ABC
Chân đường cao hạ từ S là tâm đường tròn ngoại tiếp tam giác đáy
dễ thấy H là tâm đường tròn ngoại tiếp tam giác ABC
Cho hình chóp S.ABC có SA=SB=SC và tam giác ABC vuông tại C. Gọi H là hình chiếu vuông góc của S lên mp (ABC). Khẳng định nào sau đây là khẳng định đúng?
A. H là trung điểm cạnh AB
B. H là trọng tâm tam giác ABC
C. H là trực tâm tam giác ABC
D. H là trung điểm cạnh AC.
Cho hình chóp S.ABC có hình chiếu vuông góc của S lên mặt đáy là tâm O của đường tròn ngoại tiếp tam giác ABC. Biết SB = a và góc giữa cạnh bên SA và mặt đáy bằng 60o. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC là:
A. πa 2 3
B. 4 πa 2 3
C. 2 πa 2
D. Đáp án khác
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau:
I. H là trực tâm của tam giác ABC.
II. H là trọng tâm của tam giác ABC.
III. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Số mệnh đề đúng là
A. 0
B. 1
C. 2
D. 3
Cho hình chóp tam giác đều S.ABC. Cho hình chóp tam giác đều S và có đường tròn đường tròn đáy là đường tròn nội tiếp tam giác ABC gọi là hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp đã cho là
A. 1 2
B. 1 4
C. 1 3
D. 2 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC=a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Tính thể tích khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKB là
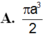
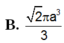
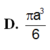
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC =a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Tính thể tích khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKB là
A . πa 3 2
B . 2 πa 3 3
C . 2 πa 3
D . πa 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC=a. Cạnh bên SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB và SC. Tính thể tích của khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKB.
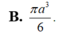
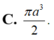
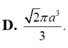
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC, SA = SB = SC = 3a. Góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp S.GBC là:
A. 6 a 3 3 25
B. 6 a 3 15 25
C. a 3 3 4
D. 4 a 3 3 5 5
Cho hình chóp S.ABCD có SA ⊥ (ABC)Tam giác ABC vuông tại B. Gọi H là chân đường vuông góc hạ từ A xuống SB. Khẳng định nào sau đây sai?
A. SA ⊥ BC
B. AH ⊥ BC
C. AH ⊥ AC
D. AH ⊥ SC
