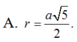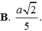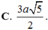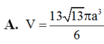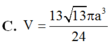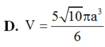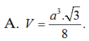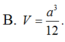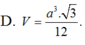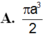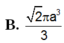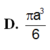Kẻ \(AH\perp BC\)
Áp dụng hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{4}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{3}}{2}\)
\(tan\widehat{SHA}=\dfrac{2}{\sqrt{3}}=\dfrac{SA}{AH}\Rightarrow SA=\dfrac{AH.2}{\sqrt{3}}=a\)
Gọi M là trung điểm BC và N là trung điểm SA, dựng hình chữ nhật AMIN \(\Rightarrow\) I là tâm mặt cầu ngoại tiếp
\(AN=\dfrac{1}{2}SA=\dfrac{a}{2}\) ; \(AM=\dfrac{1}{2}BC=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)
\(\Rightarrow R=IA=\sqrt{AM^2+AN^2}=\dfrac{a\sqrt{5}}{2}\)
\(V=\dfrac{4}{3}\pi R^3=...\)