Đáp án C
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.
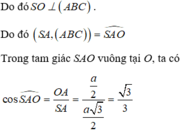
Đáp án C
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.
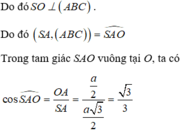

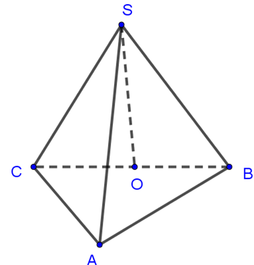
Cho hình chóp S.ABC có SA = SB = SC = a 3 2 đáy là tam giác vuông tại A, cạnh BC = a. Tính côsin của góc giữa đường thẳng SA và mặt phẳng (ABC)
A. 1 3
B. 1 3
C. 3 2
D. 1 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, A B = a , S A = S B = S C . Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45 0 . Tính khoảng cách từ điểm S đến mặt phẳng (ABC)
A. a 3 3
B. a 2 2
C. a 2
D. a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , A B a , S A = S B = S C . Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45 ° Tính khoảng cách từ điểm S đến mặt phẳng (ABC)
A. a 3 3
B. a 2 2
C. a 2
D. a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,SA vuông góc với đáy. Biết S A = a , A B = a , B C = a 2 . Gọi I là trung điểm của BC. Cosin của góc giữa 2 đường thẳng A I v à S C là:
A. − 2 3
B. 2 3
C. a 3 3 6
D. a 3 3 12
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA vuông góc với mặt phẳng đáy và SA=2a Gọi M là trung điểm của SC. Tính cosin của góc α là góc giữa đường thẳng BM và mặt phẳng (ABC).
A. cos α = 7 14
B. cos α = 2 7 7
C. cos α = 5 7
D. cos α = 21 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB= a 10 ;BC=2a;SC=2a 3 Thể tích khối chóp S.ABC là:
A. 3 a 3 2
B. 3 a 3 2
C. 3 a 3
D. a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a 2 , SA = SB = SC . Góc giữa SA và mặt phẳng (ABC) bằng 60 0 . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC theo a.
A. 2 a 3
B. a 3 2
C. 2 a 3 5
D. 2 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), AB = a, B C = a 3 , SA = a. Một mặt phẳng (α) qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a.
A. V S . A H K = a 3 3 20
B. V S . A H K = a 3 3 30
C. V S . A H K = a 3 3 60
D. V S . A H K = a 3 3 90
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), A B = a , B C = a 3 , S A = a . Một mặt phẳng α qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a
A. V S . A H K = a 3 3 20
B. V S . A H K = a 3 3 30
C. V S . A H K = a 3 3 60
D. V S . A H K = a 3 3 90