Các câu hỏi tương tự
Cho hình chóp
S
.
A
B
C
có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, H là hình chiếu của I lên SC. Khẳng định nào sau đây đúng? A.
B
I
H
⊥
S
B
C
B.
S
A
C
⊥...
Đọc tiếp
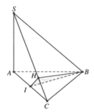
Cho hình chóp S . A B C có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, H là hình chiếu của I lên SC. Khẳng định nào sau đây đúng?
A. B I H ⊥ S B C
B. S A C ⊥ S A B
C. S B C ⊥ A B C
D. S A C ⊥ S B C
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại
A
,
AB
2
a
,
AC
2
a
. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy (ABC) một góc
45
o
.
Khoảng cách từ A đến mặt phẳng (SBC) là A.
3
a
11...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB = 2 a , AC = 2 a . Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy (ABC) một góc 45 o . Khoảng cách từ A đến mặt phẳng (SBC) là
A. 3 a 11
B. 2 5 a 11
C. 5 a 11
D. 2 3 a 11
Cho hình chóp S ABC . có đáy ABC là tam giác vuông tại A, cạnh bên SA vuông góc với
(
A
B
C
)
. Gọi I là trung điểm cạnh AC , H là hình chiếu của I trên SC . Khẳng định nào sau đây đúng? A.
(
S
B
C
)
⊥
(
I
H
B
)
B.
(
S
A
C
)
⊥
(
S
A
B
)
C. ...
Đọc tiếp
Cho hình chóp S ABC . có đáy ABC là tam giác vuông tại A, cạnh bên SA vuông góc với ( A B C ) . Gọi I là trung điểm cạnh AC , H là hình chiếu của I trên SC . Khẳng định nào sau đây đúng?
A. ( S B C ) ⊥ ( I H B )
B. ( S A C ) ⊥ ( S A B )
C. ( S A C ) ⊥ ( S B C )
D. ( S B C ) ⊥ ( S A B )
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là một điểm nằm trên đoạn thẳng BC. Mặt phẳng (SAB) tạo với (SBC) một góc
60
o
và mặt phẳng (SAC) tạo với (SBC) một góc
φ
thỏa mãn
cos
φ
2
4
. Gọi
α
là góc tạo bởi SA và mặt phẳng (ABC). Tính
tan
α...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là một điểm nằm trên đoạn thẳng BC. Mặt phẳng (SAB) tạo với (SBC) một góc 60 o và mặt phẳng (SAC) tạo với (SBC) một góc φ thỏa mãn cos φ = 2 4 . Gọi α là góc tạo bởi SA và mặt phẳng (ABC). Tính tan α
A. 3 3
B. 2 2
C. 1 2
D. 3
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B,
A
C
a
2
, mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng
60
0
. Tính theo a thể tích V của khối chóp S.ABC A.
V
3
a
3
2
B. ...
Đọc tiếp
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, A C = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 0 . Tính theo a thể tích V của khối chóp S.ABC
A. V = 3 a 3 2
B. V = 3 a 3 4
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho hình chóp S.ABC có tam giác ABC vuông cân tại
B
,
A
C
a
2
,
mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên
S
A
B
,
S
B
C
tạo với mặt đáy các góc bằng nhau và bằng
60
°
.
Tính theo a thể tích V của...
Đọc tiếp
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B , A C = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên S A B , S B C tạo với mặt đáy các góc bằng nhau và bằng 60 ° . Tính theo a thể tích V của khối chóp S.ABC
A. V = 3 a 3 2
B. V = 3 a 3 4 V = 3 a 3 12
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A,
A
B
a
,
A
D
2
a
. Hình chiếu của S lên mặt phẳng
A
B
C
là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy
A
B
C
một góc
45
°
. Khoảng cách từ A đến mặt...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, A B = a , A D = 2 a . Hình chiếu của S lên mặt phẳng A B C là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy A B C một góc 45 ° . Khoảng cách từ A đến mặt phẳng S B C là
A. 5 a 11
B. 2 5 a 11
C. 2 3 a 11
D. 3 a 11
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, ABa, BC2a, cạnh bên SA vuông góc với mặt đáy (ABC) và SA3a. Gọi
α
là góc giữa hai mặt phẳng (SAC) và (SBC). Tính sin. A.
sin
α
1
3
B.
sin
α
4138
120
C.
sin
α
13
7
D.
sin...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a, cạnh bên SA vuông góc với mặt đáy (ABC) và SA=3a. Gọi α là góc giữa hai mặt phẳng (SAC) và (SBC). Tính sin.
A. sin α = 1 3
B. sin α = 4138 120
C. sin α = 13 7
D. sin α = 7 5
Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh a. Các mặt bên (SAB), (SAC), (SBC) lần lượt tạo với đáy các góc lần lượt là
30
°
;
45
°
;
60
°
Tính thể tích của khối chóp S.ABC. Biết rằng hình chiếu vuông góc của S trên (ABC) nằm trong tam giác ABC
A
.
V
a
3
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh a. Các mặt bên (SAB), (SAC), (SBC) lần lượt tạo với đáy các góc lần lượt là 30 ° ; 45 ° ; 60 ° Tính thể tích của khối chóp S.ABC. Biết rằng hình chiếu vuông góc của S trên (ABC) nằm trong tam giác ABC
A . V = a 3 3 8 ( 4 + 3 )
B . V = a 3 3 ( 4 + 3 )
C . V = a 3 3 4 ( 4 + 3 )
D . V = a 3 3 2 ( 4 + 3 )