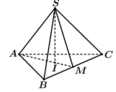
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Vì S.ABC là khối chóp đều nên suy ra S I ⊥ ( A B C )
Gọi M là trung điểm của BC
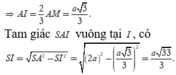
Diện tích tam giác ABC là: ![]()
Vậy thể tích khối chóp ![]()
Chọn C.

Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Vì S.ABC là khối chóp đều nên suy ra S I ⊥ ( A B C )
Gọi M là trung điểm của BC
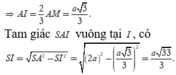
Diện tích tam giác ABC là: ![]()
Vậy thể tích khối chóp ![]()
Chọn C.
Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.
A. V = a 3 2 2
B. V = a 3 2 6
C. V = a 3 14 2
D. V = a 3 14 6
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng a 21 6 , tính theo a thể tích V của hình chóp đã cho
A. V = a 3 3 8
B. V = a 3 3 6
C. V = a 3 3 12
D. V = a 3 3 24
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính theo a thể tích V của khối chóp S.ABC
A. V = a 3 3 4
B. V = a 3 3 12
C. V = a 3 12
D. V = a 3 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và S A = a 3 . Tính thể tích V của khối chóp S.ABC
A. V = a 2 2
B. V = a 2 4
C. V = 3 a 2 4
D. V = 3 a 2 2
Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên tạo với đáy một góc 45 ° . Tính thể tích V của khối chóp S.ABC.
A. V = a 3 12
B. V = a 3 8
C. V = a 3 24
D. V = a 3 4
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng 12, mặt bên tạo với đáy một góc 45 0 . Tính thể tích V của khối chóp S.ABC
A. V = 72
B. V = 64
C. V = 56
D. V = 216
Cho hình chóp tam giác đều S.ABC đỉnh S. Có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm của cạnh BC. Tính thể tích V của khối chóp S.ABI.
A. V = a 3 11 12
B. V = a 3 11 24
C. V = a 3 11 8
D. V = a 3 11 6
Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và S A = a 2 . Thể tích V của khối chóp S.ABC là
A. 3 a 3 12
B. 6 a 3 4
C. 3 a 3 4
D. 6 a 3 12
Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và SA = a 2 . Thể tích V của khối chóp S.ABC là
A. 6 a 3 4
B. 6 a 3 12
C. 3 a 3 12
D. 3 a 3 4