Các câu hỏi tương tự
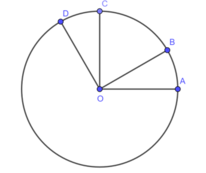
Cho hình bs.4. Biết ∠ DOA = 120 ° , OA vuông góc với OC, OB vuông góc với OD. Đọc tên các góc ở tâm có số đo nhỏ hơn 1800.
Cho hình bs.4. Biết ∠ DOA = 120 ° , OA vuông góc với OC, OB vuông góc với OD. So sánh hai cung nhỏ AB và BC.
Cho hình bs.4. Biết ∠ DOA = 120 ° , OA vuông góc với OC, OB vuông góc với OD. Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
Cho đường tròn (O;R) hai bán kính OA, OB vuông góc với nhau. Vẽ hai dây AM, BN bằng nhau và cắt nhau tại C ở trong (O) (M,N thuộc cung nhỏ AB).
a. Chứng minh: OC vuông góc với AB
b. Chúng minh tứ giác ANMB là hình thang cân
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ
∠
BC
1
6
sđ
∠
BA; sđ
∠
BD
1
2
sđ
∠
BA; sđ
∠
BE
2
3
sđ
∠
BA. Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn...
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ ∠ BC = 1 6 sđ ∠ BA; sđ ∠ BD = 1 2 sđ ∠ BA; sđ ∠ BE = 2 3 sđ ∠ BA. Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 180 ° ).
Cho hình thang ABCD có góc A = góc D = 90 độ và hai đường chéo vuông góc với nhau tại O.
a/Chứng minh hình thang này có chiều cao bằng trung bình nhân của hai đáy. Nghĩ là chứng minh AD=\(\sqrt{AB.CD}\)
b/Cho AB bằng 9 cm CD = 16 cm Tính diện tích hình thang ABCD
c/Tính độ dài các đoạn thẳng OA,OB,OC,OD
cho hình thang abcd có a=d=90 và 2 đường chéo vuông góc với nhau tại o ?
a/chứng minh hình thang này có chiều cao bằng trung bình nhân 2 đáy
b/cho ab=9, cd=16 tinh Sabcd
c/tính độ dài các đoạn thẳng oa,ob,oc,od ?
Cho (O; R) và hai bán kính OA và OB vuông góc với nhau. Vẽ dây AM và BN bằng
nhau đồng thời cắt nhau tại C ở trong (O) (M, N thuộc cung nhỏ AB).
a) Chứng minh: OC ⊥ AB.
b) Chứng minh tứ giác ANMB là hình thang cân.
Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng: OC vuông góc với AB