Chọn C
Phương pháp:
ABCD là hình bình hành khi và chỉ khi A, B, C, D phân biệt, không thẳng hàng và ![]()
Cách giải:
ABCD là hình bình hành
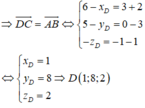
Chọn C
Phương pháp:
ABCD là hình bình hành khi và chỉ khi A, B, C, D phân biệt, không thẳng hàng và ![]()
Cách giải:
ABCD là hình bình hành
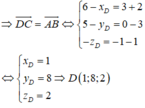
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Trong không gian Oxyz, cho hình bình hành ABCD với A(0;1;-2), B(3;-2;1), D(1;4;2). Tọa độ của điểm C là:
A. (4;1;5)
B. (4;3;1)
C. (4;2;3)
D. (4;1;1)
Cho tam giác ABC có A(1;-2;0); B(2;1;-2); C(0;3;4). Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.
A. (1;0;-6)
B. (-1;0;6)
C. (1;6;-2)
D. (1;6;2)
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là
![]()
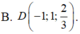
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1),B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:
A. D(-1; 1; 2 3 )
B. D(1;3;4)
C. D(1;1;4)
D. D(-1;-3;-2)
Cho 3 điểm A(1;0;1), B(2;1;-2), C(-1;3;2). Điểm D có tọa độ bao nhiêu để ABCD là hình bình hành?
A. D(-2;2;5)
B. D(1;-1;-2)
C. D(0;4;-1)
D. D(-1;-1;1)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2;3;1), B(2;1;0) và C(-3;-1;1). Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy AD và S A B C D = 3 S A B C
A. D(8;7;-1)
B. [ D ( 12 ; 1 ; - 3 ) D ( 8 ; 7 ; - 1 )
C. [ D ( - 12 ; - 1 ; 3 ) D ( 8 ; 7 ; - 1 )
D. D(-12;-1;3)
Trong không gian tọa độ Oxyz, cho ba điểm A ( - 1 ; 2 ; 2 ) ; B ( 0 ; 1 ; 3 ) ; C ( - 3 ; 4 ; 0 ) . Để tứ giác ABCD là hình bình hành thì tọa độ điểm D là
A. D(-4;5;-1).
B. D(4;5;-1).
C. D(-4;-5;-1).
D. D(4;-5;1).
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
A. a+b+c=6
B. a+b+c=5
C. a+b+c=8
D. a+b+c=7