Đáp án D
Vì ABCD là hình thang
![]()
=>Phương trình đường thẳng AD là
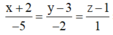
![]()
Ta có

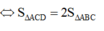
Mà diện tích tam giác ABC là
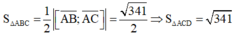
Mặt khác
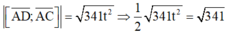

Vì ABCD là hình thang => D(-12;-1;3)
Đáp án D
Vì ABCD là hình thang
![]()
=>Phương trình đường thẳng AD là
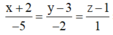
![]()
Ta có

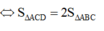
Mà diện tích tam giác ABC là
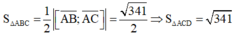
Mặt khác
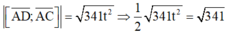

Vì ABCD là hình thang => D(-12;-1;3)
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Trong không gian tọa độ Oxyz cho các điểm A(1;2;3), B(2;1;0), C(4;-3;-2), D(3;-2;1), E(1;1;-1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
A. 1
B. 4
C. 5
D. không tồn tại
Trong không gian với hệ tọa độ Oxyz, cho hình thang ABCD có hai đáy AB, CD; có tọa độ ba đỉnh A ( 1 ; 2 ; 1 ) , B ( 2 ; 0 ; - 1 ) , C ( 6 ; 1 ; 0 ) . Biết hình thang có diện tích bằng 6 2 . Giả sử đỉnh D ( a ; b ; c ) , tìm mệnh đề đúng?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là
![]()
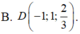
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1),B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:
A. D(-1; 1; 2 3 )
B. D(1;3;4)
C. D(1;1;4)
D. D(-1;-3;-2)
Trong không gian tọa độ Oxyz, cho các điểm A (1;2;3), B (2;1;0), C (4;3;-2), D (3;4;1), E (1;1;-1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
A. 1
B. 4.
C. 5
D. Không tồn tại.
Trong không gian với hệ trục tọa độ Oxyz ,cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B',C', D' sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB'C'D' có thể tích nhỏ nhất. Phương trình mặt phẳng (B'C'D') là
A. 16x-40y-44z+39=0
B. 16x-40y-44z-39=0
C. 16x+40y+44z-39=0
D. 16x+40y-44z+39=0
Trong không gian Oxyz, cho tam giác đều ABC với A (5;3;-1) và B (2;3;-4) điểm C nằm trong mặt phẳng Oxyz có tung độ nhỏ hơn 3.
a) Tìm tọa độ điểm D biết ABCD là tứ diện đều.
b) Tìm tọa độ điểm S biết SA, SB, SC đôi một vuông góc.
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
A. a+b+c=6
B. a+b+c=5
C. a+b+c=8
D. a+b+c=7