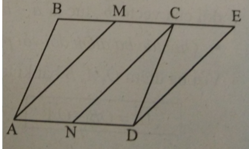
Do ABCD là hình bình hành nên: AD = BC.
Lại có; M và N lần lượt là trung điểm của BC; AD nên : AN = ND= BM = MC.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.A. AD BC . B. MQ PN . C. MN QP . D. AB DC .Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúngA. HA CD và AD CH .B....
Đọc tiếp
Câu 8: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AD và BC, có bao nhiêu vectơ bằng với DM từ các điểm đã cho? A. 3. B. 4. C. 5. D. Câu 9: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chọn khẳng định đúng trong các khẳng định sau.
A. AD BC . B. MQ PN . C. MN QP . D. AB DC .
Câu 10: Cho tam giác ABC với trực tâm H, D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng
A. HA CD và AD CH .
B. HA CD và DA HC .
C. HA CD và AD HC .
D. HA CD và AD HC và OB OD .
Câu 1: Cho ABCD là hình vuông cạnh bằng 1. Khi đó độ dài của AC bằng
A. 1. B. 2. C. 2. D. 3.
Câu 2: Cho tam giác ABC vuông tại C có cạnh AC cm BC cm 4 , 3 . Độ dài của vectơ AB là
A. 7 . cm B. 6 . cm C. 5 . cm D. 4 . cm
Câu 3: Cho hình vuông ABCD tâm O, cạnh 2a. Độ dài vectơ DO bằng
A. 2 2. a B. 2 . 2 a C. a 2. D. 2 2. a
Câu 4: Cho đoạn thẳng AB cm 10 , điểm C thỏa mãn AC CB . Độ dài vectơ AC là
A. 10 . cm B. 5 . cm C. 20 . cm D. 15 . c
Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB làA. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giácA. 4074342. B. 8148684. C. 4076361. D. 8152722
Đọc tiếp
Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB là
A. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .
Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?
A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.
Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giác
A. 4074342. B. 8148684. C. 4076361. D. 8152722
Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ M N → có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P bằng:
A. 1
B. 2
C. 3
D. 6
Cho hình bình hành ABCD với M và N lần lượt là trung điểm của BC và AD .Tìm tổng của hai vector sau:
a) AD→ và DC→
b)NA→ và ND→
c)NC→ và MC→
d)AM→ và CD→
Trong mặt phẳng Oxy cho A (2,0) B (4,0) và C ( 1,3)
a) Tìm tọa độ các vectơ AB , BC và CA
B) Chứng minh ba điểm A , B , C không thẳng hàng
C) Tìm tọa độ M , N , P lần lượt là trung điểm BC , CA và AB
ai giúp em bài này với
Cho tam giác ABC gọi M,N,P lần lượt là trung điểm của các cạnh AB,AC,BC a) Tìm các vectơ cùng phương AM b) Tìm các vectơ cùng hướng MN c) Tìm các vectơ ngược hướng BC
Cho hình vuông ABCD với P là giao điểm hai đường chéo BD và AC, M là giao điểm thỏa mãn vecto MO= vecto DC + vecto OB. Mệnh đề nào dưới đây đúng A. M đối xứng với C qua B B. M là trung điểm của AD C. M đối xứng với V qua D D. M đối xứng với A qua B
cho hình bình hành ABCD có tâm O.Gọi M,N lần lượt là trung điểm của AD,BC.Tìm tất cả các vect u thỏa mãn vectơ u = 2ON
Cho hình bình hành ABCD.Gọi M là trung điểm CD. N trên đoạn BM s/c BN=2MN
a) C/m: 3vectoAB+4vectoCD=vectoCM+vectoND+vectoMN
b) C/m vectơ AN=4/3vectoAB+2/3vectoBD
c) C/m: A,C,N thẳng hàng