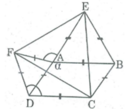
Vì ∠ (BAD) + ∠ (BAE) + ∠ (EAF) + ∠ (FAD) = 360 0
⇒ ∠ (EAF) = 360 0 – ( ∠ (BAD) + ∠ (BAE) + ∠ (FAD) )
Mà ∠ (BAD) = α 2 (gt)
∠ (BAE) = 60 0 (ΔBAE đều)
∠ (FAD) = 60 0 (ΔFAD đều)
Nên ∠ (EAF) = 360 0 – ( α 2 + 60 0 + 60 0 ) = 240 0 – α
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình bình hành ABCD có góc A = 110 độ. Ở phía ngoài của hình bình hành vẽ các tam giác đều ABE và ADF.
a) TÍnh số đo góc EAF
b) Chứng minh tam giác EAF = tam giác CDF
c) Chứng minh tam giác EFC là tam giác đều
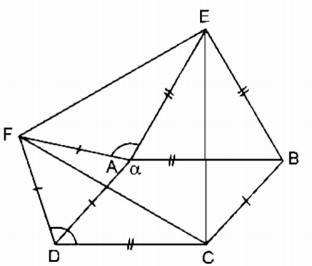
Cho hình bình hành ABCD có A = α > 90 0 . Ở phía ngoài hình bình hành vẽ các tam giác đều ADF, ABE. Chứng minh rằng tam giác CEF là tam giác đều.
Cho hình bình hành ABCD có góc \(A=\alpha>90^o\). Ở phía ngoài hình bình hành vẽ tam giác đều ADF, ABE.
a, Tính góc EAF
b, Chứng minh rằng tam giác CEF là tam giác đều
Cho hình bình hành ABCD có góc A tù. Ở phía ngoài hình bình hành ta vẽ các tam giác đều ADF, ABE.
a) Tính góc EAF; góc AEF
b) Chứng minh rằng: Tam giác CEF đều.
Giải từng bước giúp mình nhé ! Mơn nhìu!
cho hình bình hành ABCD có gốc A =a >90 độ . Ở phía ngoài hình bình hành vẽ các tam giác đều ADF , ABE
a, tính EAF
b, Chứng minh rằng tam giác CEF là tam gics đều
Cho hình bình hành ABCD có góc A=α>900. Ở phía ngoài hình bình hành, vẽ các tam giác đều ADF, ABE.
a. Tính góc EAF
b. Chứng minh rằng tam giác CEF là tam giác đều.
Cho hình bình hành ABCD , A=130 độ vẽ ở ngoài hình bình hành tam giác đều ABE và ADF
a, Tính góc EAF
b, chứng minh tam giác CEF đều
Cho hình bình hành ABCD có góc A = 1100. Ở phía ngoài của hình bình hành vẽ các tam giác đều ABE và ADF.
a) Tính số đo góc EAF
b) Chứng minh \(\Delta EAF=\Delta CDF\)
c) Chứng minh \(\Delta EFC\)là tam giác đều.
cho hình bình hành abcd có góc a = 130 độ . vẽ ở ngoài hình bình hành các tam giác đều ABE,ADF a) tính gócAEF b) cm rằng tam giác CEF là tam giác đều