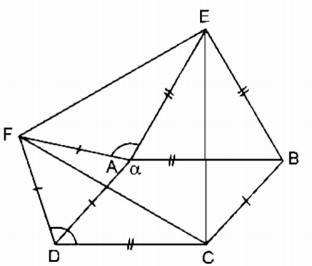
Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.