Các câu hỏi tương tự
Trọng tâm các mặt của một hình tứ diện đều tạo thành một hình đa diện mới có tên là gì
A. Tứ diện đều
B. lập phương
C. nhị thập diện đều
D. bát diện đều
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Tính S. A.
S
4
3
a
2
B.
S
2
3
a
2
C.
S
3
a
2...
Đọc tiếp
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Tính S.
A. S = 4 3 a 2
B. S = 2 3 a 2
C. S = 3 a 2
D. S = 8 a 2
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Tính S. A.
S
8
a
2
B.
S
4
3
a
2
C.
S
2
3
a
2
D.
S
3...
Đọc tiếp
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Tính S.
A. S = 8 a 2
B. S = 4 3 a 2
C. S = 2 3 a 2
D. S = 3 a 2
Cho hình bát diện đều cạnh 2. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Khi đó, S bằng A. S 32 B.
S
8
3
C.
S
4
3
D.
S
16
3
Đọc tiếp
Cho hình bát diện đều cạnh 2. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Khi đó, S bằng
A. S = 32
B. S = 8 3
C. S = 4 3
D. S = 16 3
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó.Mệnh đề nào sau đây là đúng? A.
S
4
3
a
2
B.
S
3
a
2
C.
S
2
3
a
2
D.
S
8
a
2
Đọc tiếp
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó.
Mệnh đề nào sau đây là đúng?
A. S = 4 3 a 2
B. S = 3 a 2
C. S = 2 3 a 2
D. S = 8 a 2
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ) A.
V
a
3
2
.
B.
V
a
3
2
4
.
C.
V
a...
Đọc tiếp
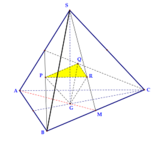
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ)
A. V = a 3 2 .
B. V = a 3 2 4 .
C. V = a 3 2 2 .
D. V = a 3 2 8 .
H
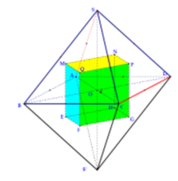
Cho hình lập phương . Gọi
H
là hình bát diện đều có các đỉnh là tâm các mặt của
H
. Tính tỉ số thể tích của
H
và
H
. A.
1
2
B.
1
4
C.
1
6
D.
1
12
Đọc tiếp
H Cho hình lập phương . Gọi H ' là hình bát diện đều có các đỉnh là tâm các mặt của H . Tính tỉ số thể tích của H ' và H .
A. 1 2
B. 1 4
C. 1 6
D. 1 12
Cho hình lập phương
H
. Gọi
H
là hình bát diện đều có các đỉnh là tâm các mặt của
H
. Tính tỉ số thể tích của
H
và
H
. A.
1
2
B.
1
4
C.
1...
Đọc tiếp
Cho hình lập phương H . Gọi H ' là hình bát diện đều có các đỉnh là tâm các mặt của H . Tính tỉ số thể tích của H ' và H .
A. 1 2
B. 1 4
C. 1 6
D. 1 12
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.Số mệnh đề đúng là A. 3 B. 2 C. 0 D. 1
Đọc tiếp
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là
A. 3
B. 2
C. 0
D. 1