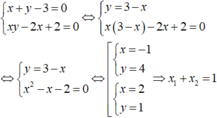Các câu hỏi tương tự
Hệ phương trình:
x
+
y
+
2
y
-
1
+
x
-
y
5...
Đọc tiếp
Hệ phương trình: x + y + 2 y - 1 + x - y = 5 y 2 + 2 = x y + y có cặp nghiệm duy nhất (x;y). Tính x + 3y.
A. 2
B. 4
C. 5
D. 7
Phương trình
4
x
-
2
x
+
1
+
2
(
2
x
-
1
)
sin
(
2
x
+
y
-
1
)
+
2
0
có nghiệm xa, yb. A.
S
π
2...
Đọc tiếp
Phương trình 4 x - 2 x + 1 + 2 ( 2 x - 1 ) sin ( 2 x + y - 1 ) + 2 = 0 có nghiệm x=a, y=b.
A. S = π 2 + k π
B. S = - π 2 + k 2 π
C. S = π 3 + k π
D. S = - π 3 + k 2 π
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;-2;3) và hai mặt phẳng (P):x+y+z+10;(Q):x-y+z-20. Phương trình nào dưới đây là phương trình đường thẳng qua A, song song với (P) và (Q). A.
x
1
+
2
t
y
-
2...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;-2;3) và hai mặt phẳng (P):x+y+z+1=0;(Q):x-y+z-2=0. Phương trình nào dưới đây là phương trình đường thẳng qua A, song song với (P) và (Q).
A. x = 1 + 2 t y = - 2 z = 3 + 2 t
B. x = - 1 + t y = 2 z = - 3 - t
C. x = 1 y = - 2 z = 3 - 2 t
D. x = 1 + t y = - 2 z = 3 - t
Cho phương trình
y
x
3
-
6
x
2
+
9
x
-
2
và các phát biểu sau:(1) x 0 là nghiệm duy nhất của phương trình(2) Phương trình có nghiệm dương (3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1(4) Phương trình trên có tổng 2 nghiệm là:
-
log...
Đọc tiếp
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Cho hàm số y=f'(x) là dạng dường cong hình bên và f(-1)=-2, f(1)=1 khi đó phương trình f(x)=0 có bao nhiêu nghiệm?
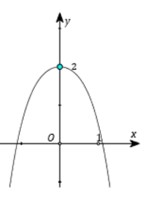
A. 1
B. 2
C. 3
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x + 2 y + 3 z - 5 = 0 . Đường thẳng Δ vuông góc với (P) cắt d 1 và d 2 có phương trình là:
A. ∆ : x - 1 1 = y + 1 2 = z 3
B. ∆ : x - 2 1 = y - 3 2 = z - 1 3
C. ∆ : x - 3 1 = y - 3 2 = z + 2 3
C. ∆ : x - 1 3 = y + 1 2 = z 1
Cho hàm số yf(x) có bảng biến thiên như sauSố nghiệm của phương trình f( 2-x)-1 0 là A. 0 B. 2 C. 1 D. 3
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như sau
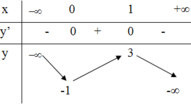
Số nghiệm của phương trình f( 2-x)-1 = 0 là
A. 0
B. 2
C. 1
D. 3
Phương trình
4
x
-
2
x
+
1
+
2
2
x
-
1
sin
2
x
+
y
-
1
+
2
0
có...
Đọc tiếp
Phương trình 4 x - 2 x + 1 + 2 2 x - 1 sin 2 x + y - 1 + 2 = 0 có nghiệm x = a y = b . Tính S = a + b
A. S = π 2 + k π
B. S = - π 2 + k 2 π
C. S = π 3 + k π
D. S = - π 3 + k 2 π
Cho hàm số y f (x) liên tục trên R có đồ thị như hình vẽ. Biết trên
(
-
∞
;
-
3
)
∪
(
2
;
+
∞
)
t
h
ì
f
(
x
)
0
. Số nghiệm nguyên thuộc (-10; 10) của bất phương trình
[
f
(
x
)...
Đọc tiếp
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
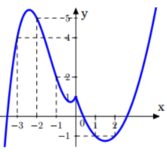
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Đường thẳng (d) vuông góc với
m
p
(
P
)
:
x
+
y
+
z
+
1
0
và cắt cả 2 đường thẳng
x
-
1
2
y
+
1
-
1
z
và
d
2
:
x...
Đọc tiếp
Đường thẳng (d) vuông góc với m p ( P ) : x + y + z + 1 = 0 và cắt cả 2 đường thẳng x - 1 2 = y + 1 - 1 = z và d 2 : x - 2 y + z - 1 = 0 2 x - y - 2 z + 1 = 0 có phương trình là:
A. 2 x + y - 3 z + 1 = 0 x - 2 y + z = 0
B. 2 x + y - 3 z - 1 = 0 x - 2 y + z - 1 = 0
C. x + y - 3 z - 1 = 0 2 x - 2 y + z - 1 = 0
D. x + y - 3 z + 1 = 0 2 x - 2 y + z = 0