Ta có: x + y = 4 x 2 + y 2 = m 2 ⇒ 4 2 − 2 P = m 2 ⇔ P = 16 − m 2 2
⇒ S 2 − 4 P = 16 − 2 16 − m 2 = 2 m 2 − 16 ≥ 0 ⇔ m ≥ 8
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hệ bất phương trình
x
-
7
≤
0
mx
≥
m
+
1
Xét các mệnh đề sau : (1) : Với m 0 , hệ luôn có nghiệm. (2) : Với 0 ≤ m 1/6 hệ vô nghiệm. (3) : Với m 1/6 hệ có nghiệm duy nhất. Mệ...
Đọc tiếp
Cho hệ bất phương trình x - 7 ≤ 0 mx ≥ m + 1
Xét các mệnh đề sau :
(1) : Với m< 0 , hệ luôn có nghiệm.
(2) : Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) : Với m = 1/6 hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D. (1) ; (2) và (3)
Cho hệ bất phương trình
x
-
7
≤
0
m
x
≥
m
+
1
. Xét cá...
Đọc tiếp
Cho hệ bất phương trình x - 7 ≤ 0 m x ≥ m + 1 . Xét các mệnh đề sau
(1) Với m< 0 , hệ luôn có nghiệm.
(2) Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) Với m= 1/6 , hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D . Cả ba đúng
Cho hệ phương trình
x
+
y
m
+
1
x
2
y
+
y
2
x
2
m...
Đọc tiếp
Cho hệ phương trình x + y = m + 1 x 2 y + y 2 x = 2 m 2 - m - 3 và các mệnh đề:
(I) Hệ có vô số nghiệm khi m = -1.
(II) Hệ có nghiệm khi m > 3 2
(III) Hệ có nghiệm với mọi m.
Các mệnh đề nào đúng?
A. Chỉ (I).
B. Chỉ (II).
C. Chỉ (III).
D. Chỉ (I) và (III).
Cho hệ phương trình
x
+
y
m
+
1
x
2
y
+
y
2
x...
Đọc tiếp
Cho hệ phương trình x + y = m + 1 x 2 y + y 2 x = 2 m 2 − m − 3 và các mệnh đề :
(I) Hệ có vô số nghiệm khi m = - 1
(II) Hệ có nghiệm khi m > 3 2
(III) Hệ có nghiệm với mọi m .
Các mệnh đề nào đúng ?
A. Chỉ (I).
B. Chỉ (II).
C. Chỉ (III)
D. Chỉ (I) và (III).
Cho hệ phương trình:
m
x
+
3
m
−
2
y
+
m
−
3
0...
Đọc tiếp
Cho hệ phương trình: m x + 3 m − 2 y + m − 3 = 0 2 x + m + 1 y − 4 = 0 . Hệ thức liên hệ giữa x và y độc lập đối với tham số m khi hệ phương trình có nghiệm duy nhất là:
A. x = − 1 + 15 6 y
B. y = − 1 − 15 6 x
C. x = − 1 − 15 6 y
D. y = − 1 + 15 6 x
Cho hệ bất phương trình
mx
+
2
m
0
2
x
+
3
5...
Đọc tiếp
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R
(III) Khi m≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là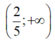 
(IV) Khi m> 0 thì hệ bất phương trình đã cho có tập nghiệm là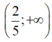 
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
3, Cho hệ phương trình:
\(\left\{{}\begin{matrix}3x^2+2xy+y^2=11\\x^2+2xy+3y^2=17+m\end{matrix}\right.\)
a) Giải hệ phương trình với m = 0
b) Tìm m để hệ phương trình có nghiệm
Cho hệ phương trình:
m
x
−
y
2
3
x
+
m
y
5
(
m
≠
0
)
....
Đọc tiếp
Cho hệ phương trình: m x − y = 2 3 x + m y = 5 ( m ≠ 0 ) . Giá trị của m để hệ phương trình có nghiệm duy nhất thỏa mãn x + y < 1 là:
A. m > 7 + 33 2 m < 7 − 33 2
B. m > − 7 + 33 2 m < − 7 − 33 2
C. − 7 − 33 2 < m < − 7 + 33 2
D. 7 − 33 2 < m < 7 + 33 2
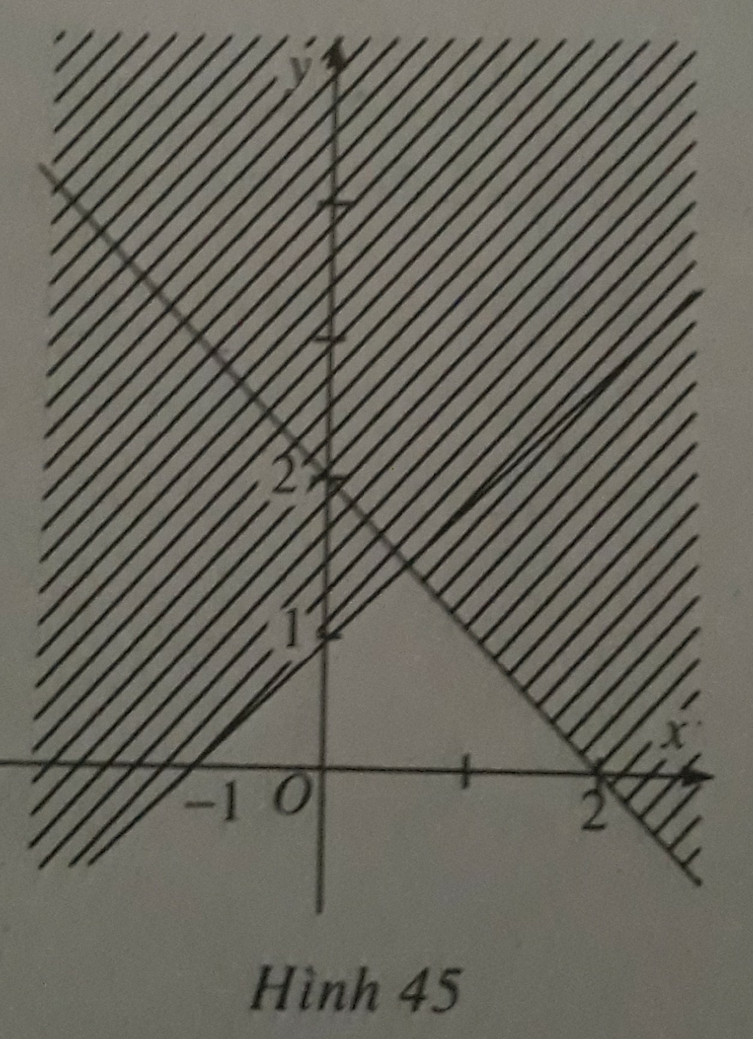
Trong các khẳng định sau, khẳng định nào đúng?A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2. B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trìnhvà (x; y) (-1; 1) là một nghiệm của hệ. C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình và (x; y) (-2; 1) là một nghiệm của hệ. D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình và...
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng?
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình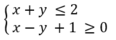 
và (x; y) = (1; 0) là một nghiệm của hệ.
Cho hệ phương trình:
x
−
m
y
0
m
x
−
y
m
+
1
. Hệ phương trình có vô số nghiệm khi: A....
Đọc tiếp
Cho hệ phương trình: x − m y = 0 m x − y = m + 1 . Hệ phương trình có vô số nghiệm khi:
A. m = ± 1
B. m = 0
C. m = − 1
D. m = 0 hoặc m = − 1