Question

Cho hbh ABCD ,O là gđ của 2 đg chéo AC và BD.Gọi M,N lầ lượt là trung điểm của OB và OD

a,Vẽ hình và Cminh:AMNC là hbh

b,Tia AM cắt  BC ở E,tia CN cắt AD ở F

c,Cminh:3 đoạn thẳng AC,BD và EF đồng quy

Answer 1

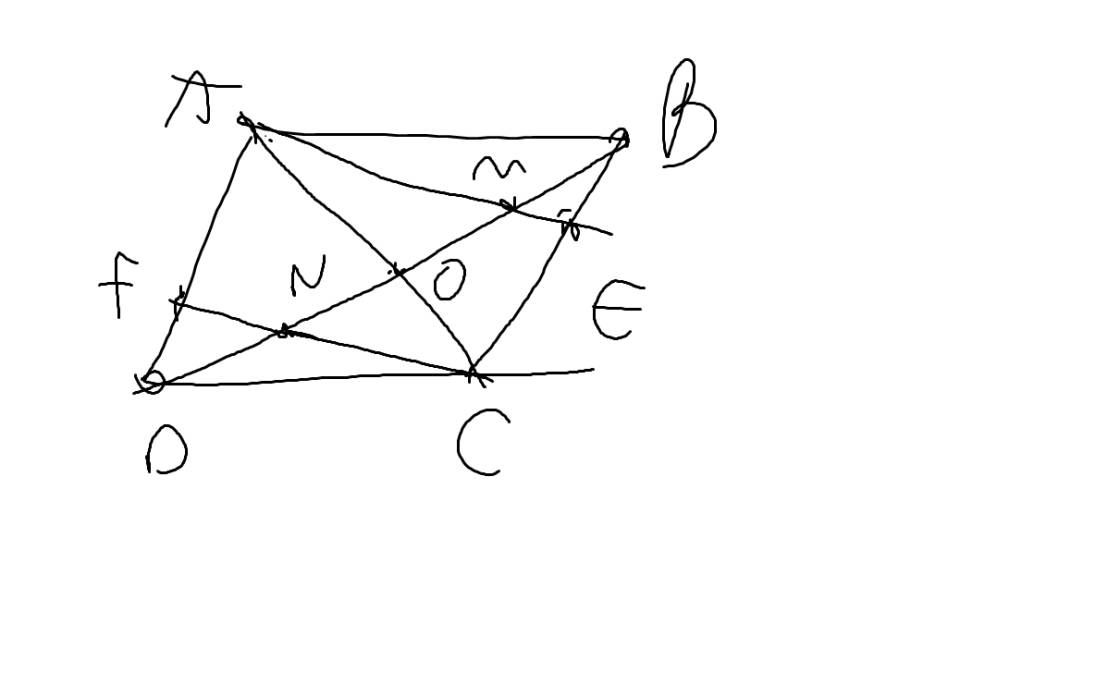
a: ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

O là trung điểm của BD

=>BO=DO(1)

M là trung điểm của OB

=>\(OM=MB=\dfrac{OB}{2}\left(2\right)\)

N là trung điểm của DO

=>\(DN=NO=\dfrac{DO}{2}\left(3\right)\)

Từ (1),(2),(3) suy ra BM=MO=NO=DN

MO=NO

=>O là trung điểm của MN

Xét tứ giác AMCN có

O là trung điểm chung của AC và MN

=>AMCN là hình bình hành

c: AMCN là hình bình hành

=>AM//CN

=>AE//CF

Xét tứ giác AECF có

AE//CF

AF//CE

Do đó: AECF là hình bình hành

=>AC cắt EF tại trung điểm của mỗi đường

mà O là trung điểm của AC

nên O là trung điểm của EF

=>AC,BD,EF đồng quy tại O