Chọn C.
Dựa vào BBT ta thấy đường thẳng y = -2018 nằm dưới điểm cực tiểu của đồ thị hàm số, suy ra đường thẳng y = -2018 cắt đồ tị hàm số tại 2 điểm
Cho hàm số y =f(x) xác định và liên tục trên ℝ , có bảng biến thiên như hình vẽ bên. Đồ thị hàm số y = f(x) cắt đường thẳng y = - 2018 tại bao nhiêu điểm?
A. 2
B. 4
C. 0
D. 1
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như hình dưới đây. Đồ thị của hàm số y=f(x) cắt đường thẳng y=-2019 tại bao nhiêu điểm
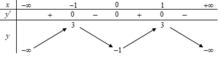
A. 1.
B. 2
C. 4.
D. 3
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có bảng biến thiên như hình bên. Đồ thị hàm số y=f(x) cắt đường thẳngy=2019 tại bao nhiêu điểm?
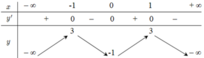
A. 2
B. 1
C. 0
D. 4
Cho hàm số y = f x xác định, liên tục trên ℝ và có bảng biến thiên như hình bên. Đồ thị hàm số y = f x cắt đường thẳng y = - 2018 tại bao nhiêu điểm?
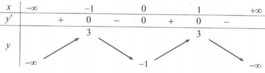
A. 2
B. 4
C. 1
D. 0
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
Đồ thị hàm số y = | f ( x ) | có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Cho hàm số y=f(x) xác định và liên tục trên các khoảng ( - ∞ ; 0 ) , ( 0 ; + ∞ ) và có bảng biến thiên như sau
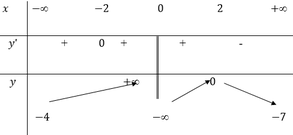
Tìm tất cả các giá trị thực của m để đường thẳng y=m cắt đổ thị hàm số y=f(x) tại 3 điểm phân biệt
A. - 4 ≤ m < 0
B. - 4 < m < 0
C. - 7 < m < 0
D. - 4 < m ≤ 0
Cho hàm số y=f(x) xác định trên R\{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận
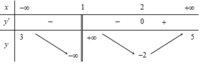
A. 1.
B. 2
C. 3
D. 4
Cho hàm số y=f(x) liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ bên. Hỏi số đường tiệm cận đứng của đồ thị hàm số y = 1 e f 2 x - 2 là bao nhiêu?
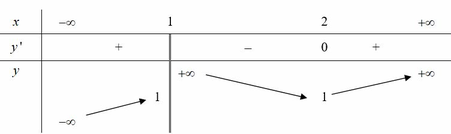
A. 0
B. 3
C. 1
D. 2
Cho hàm số y=f(x) xác đinh, liên tục trên ~ và có bảng biến thiên như sau:
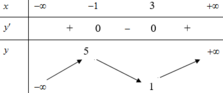
Đồ thị hàm số y = | f ( x ) | có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 4
D. 5
