Đáp án D
Dễ thấy 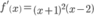
Do f (x) đổi dấu từ âm sang dương khi qua điểm x = 2 nên f (x) đạt cực trị tại x =2
Hàm số f (x) nghịch biến trên do 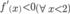
Đặt 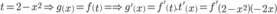
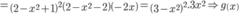
đồng biến trên 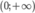
Đáp án D
Dễ thấy 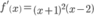
Do f (x) đổi dấu từ âm sang dương khi qua điểm x = 2 nên f (x) đạt cực trị tại x =2
Hàm số f (x) nghịch biến trên do 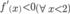
Đặt 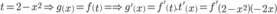
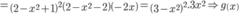
đồng biến trên 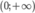
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y = f(x) , có đạo hàm là f '(x) liên tục trên ℝ và hàm số f '(x) có đồ thị như hình dưới đây.
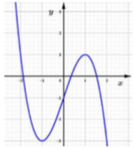
Hỏi hàm số y = f(x) có bao nhiêu cực trị?
A. 1.
B. 0.
C. 3.
D. 2.
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f’(x) như hình vẽ bên. Hàm số g x = f x - x 3 3 + x 2 - x + 2 đạt cực đại tại
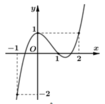
A. x = -1
B. x = 0
C. x = 1
D. x = 2
Cho hàm số y=f’(x) liên tục và có đạo hàm trên ℝ đồ thj hàm số y=f’(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
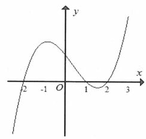
A. - ∞ ; - 2
B. - 1 ; 1
C. 2 ; + ∞
D. - ∞ ; - 1
Cho hàm số y=f(x) có đạo hàm trên ℝ. Đường cong trong hình vẽ bên là đồ thị của hàm số y=f’(x), f’(x) liên tục trên ℝ. Xét hàm số g x = f x 2 - 2 . Mệnh đề nào dưới đây sai?
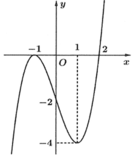
A. Hàm số g(x) nghịch biến trên khoảng (-∞;2)
B. Hàm số g(x) đồng biến trên khoảng (2;+∞)
C. Hàm số g(x) nghịch biến trên khoảng (-1;0)
D. Hàm số g(x) nghịch biến trên khoảng (0;2)
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên ℝ . Biết f ' − 2 = − 8 , f ' 1 = 4 và đồ thị của hàm số f"(x) như hình vẽ dưới đây. Hàm số y = 2 f x − 3 + 16 x + 1 đạt giá trị lớn nhất tại x 0 thuộc khoảng nào sau đây?
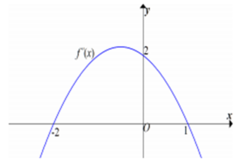
A. 0 ; 4
B. 4 ; + ∞
C. − ∞ ; 1
D. − 2 ; 1
Cho hàm sốy =f(x), y =g(x)liên tục trên ℝ và có đồ thị các đạo hàm (đồ thị y =g’(x) là đường đậm hơn) như hình vẽ
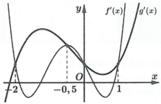
Hàm số h(x) =f(x-1) –g(x-1) nghịch biến trên khoảng nào dưới đây?
A. (1/2;1).
B. (-1;1/2).
C. (1;+∞).
D. (2;+∞)
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: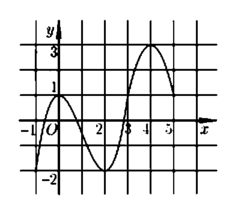
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2