Chọn A.
Ta có: y’ = ex+ xex
Và y’’= ex+ ex+xex= 2ex+ xex
Do đó: y’’= 2y’- y
Chọn A.
Ta có: y’ = ex+ xex
Và y’’= ex+ ex+xex= 2ex+ xex
Do đó: y’’= 2y’- y
Cho hàm số y = ln 1 x + 1 . Đẳng thức nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho x, y là các số thực dương thỏa mãn 9ln2 x + 4ln2 y = 12ln x.ln y. Đẳng thức nào sau đây là đúng?
A. x2 = y3
B. 3x = 2y
C. x3 = y2
D. x = y
Cho x, y là các số thực dương thỏa mãn log 3 2 x + y + 1 x + y = x + 2 y . Tìm giá trị nhỏ nhất của biểu thức T = 1 x + 2 y
A. 3 + 3
B. 4
C. 3 + 2 3
D. 6
Cho hàm số f x = x 4 + a x 3 + b x 2 + c x + 1 . Biết rằng đồ thị hàm số y = f(x) có ít nhất một giao điểm với trục hoành. Bất đẳng thức nào sau đây là đúng?
![]()
![]()
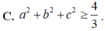
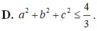
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y
Tìm giá trị P m a x của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
![]()
![]()
![]()
![]()
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) x y .
Tìm giá trị P m a x của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
![]()
![]()
![]()
![]()
Cho hai số dương x, y thỏa mãn l o g 2 ( 4 x + y + 2 x y + 2 ) y + 2 = 8 - 2 x - 2 y + 2 . Giá trị nhỏ nhất của P = 2 x + y là số có dạng M = a b + c với a , b ∈ ℕ , a > 2 . Tính S = a + b + c
A. 17
B. 7
C. 19
D. 3
Cho hai số thực x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất của biểu thức P = x + 2 y + 3 x + y + 6
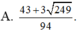
![]()
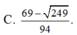
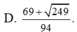
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x − 2 y + 3 z − 1 = 0 và đường thẳng d : x − 1 3 = y − 2 3 = z − 3 1 . Mệnh đề nào sau đây là đúng?
A. Đường thẳng d cắt mặt phẳng (P).
B. Đường thẳng d song song với mặt phẳng (P).
C. Đường thẳng d nằm trong mặt phẳng (P).
D. Đường thẳng d vuông góc với mặt phẳng (P).