Các câu hỏi tương tự
Cho hàm số yf(x). Hàm số yf’(x) có đồ thị như hình vẽ:Bất phương trình
f
x
36
+
x
+
3
-
2
x
-
1
m
đúng với mọi mÎ(0;1) khi và chỉ khi A. ...
Đọc tiếp
Cho hàm số y=f(x). Hàm số y=f’(x) có đồ thị như hình vẽ:
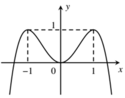
Bất phương trình f x 36 + x + 3 - 2 x - 1 > m đúng với mọi mÎ(0;1) khi và chỉ khi
A. m ≤ f 1 + 9 36
B. m < f 1 + 9 36
C. m > f 1 + 9 36
D. m ≥ f 1 + 9 36
Có bao nhiêu giá trị nguyên của tham số mÎ[-2018;2019] để đồ thị hàm số y = x 3 - 3 m x + 3 và đường thẳng y = 3 x + 1 có duy nhất một điểm chung?
A. 1
B. 2019
C. 4038
D. 2018
Có bao nhiêu giá trị nguyên của tham số mÎ(−2018;2018) để hàm số
y
2
x
-
6
x
-
m
đồng biến trên khoảng (5;+¥) ? A. 2018 . B. 2021. C. 2019 . D. 2020 .
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số mÎ(−2018;2018) để hàm số y = 2 x - 6 x - m đồng biến trên khoảng (5;+¥) ?
A. 2018 .
B. 2021.
C. 2019 .
D. 2020 .
Để đồ thị hàm số
(
C
)
:
y
x
3
-
2
x
2
+
(
1
-
m
)
x
+
m
(m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là
x
1
,
x
2
,
x
3...
Đọc tiếp
Để đồ thị hàm số ( C ) : y = x 3 - 2 x 2 + ( 1 - m ) x + m (m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 < 4 thì giá trị của m là:
A. m < 1
B. m > 1 m < - 1 4
C. - 1 4 < m < 1
D. - 1 4 < m < 1 m ≠ 0
Cho hàm số:
y
x
−
1
x
2
+
m
x
+
m
. Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt: A. ...
Đọc tiếp
Cho hàm số: y = x − 1 x 2 + m x + m . Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt:
A. m > 4 m < 0
B. − 1 2 ≠ m < 0
C. 0 < m < 4
D. − 1 2 ≠ m < 0 m > 4
Số giá trị nguyên của tham số mÎ[-10;10] để bất phương trình
3
+
x
+
6
-
x
-
18
+
3
x
-
x
2
≤
m
2
-
m
+
1
nghiệm đúng
∀
x
∈
[...
Đọc tiếp
Số giá trị nguyên của tham số mÎ[-10;10] để bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 nghiệm đúng ∀ x ∈ [ - 3 ; 6 ] là
A. 28
B. 20
C. 4
D. 19
Cho hàm số
y
x
+
1
x
2
+
m
x
+
1
có đồ thị (C). Tìm số nguyên dương nhỏ nhất m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt. A. m 2 B. m 4 C. m 3 D. m 1
Đọc tiếp
Cho hàm số y = x + 1 x 2 + m x + 1 có đồ thị (C). Tìm số nguyên dương nhỏ nhất m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt.
A. m = 2
B. m = 4
C. m = 3
D. m = 1
Có bao nhiêu giá trị nguyên của tham số mÎ[-10;10] để bất phương trình sau nghiệm đúng
∀
x
∈
R
:
6
+
2
7
x
+
2
-
m
3
-
7...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số mÎ[-10;10] để bất phương trình sau nghiệm đúng ∀ x ∈ R : 6 + 2 7 x + 2 - m 3 - 7 x - m + 1 2 x ≥ 0
A. 10
B. 9
C. 12
D. 11
Cho hàm số
y
x
−
2
x
−
3
có đồ thị (C). Tìm m để đường thẳng d đi qua
A
(
0
;
m
)
có hệ góc bằng 2 cắt (C) tại 2 điểm phâ...
Đọc tiếp
Cho hàm số y = x − 2 x − 3 có đồ thị (C). Tìm m để đường thẳng d đi qua A ( 0 ; m ) có hệ góc bằng 2 cắt (C) tại 2 điểm phân biệt có hoành độ dương
A. m ∈ ℝ .
B. 2 3 < m < 7 .
C. m < 2 3 .
D. m > 7 .




