Đáp án B
Tập xác định D = R
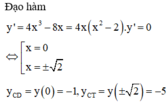
h 1 , h 2 lần lượt là khoảng cách từ 2 điểm cực đại và cực tiểu của đồ thị hàm số đến trục hoành, do đó
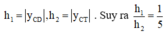
Đáp án B
Tập xác định D = R
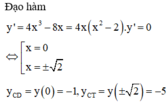
h 1 , h 2 lần lượt là khoảng cách từ 2 điểm cực đại và cực tiểu của đồ thị hàm số đến trục hoành, do đó
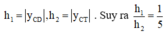
Cho hàm số y = x 4 − 4 x 2 − 1 . Gọi h 1 , h 2 lần lượt là khoảng cách từ hai điểm cực đại và cực tiểu của đồ thị hàm số đến trục hoành. Khi đó tỷ số h 1 h 2 bằng
A. 5
B. 1 2
C. − 1 5
D. 1 5
Cho hàm số y = x 4 − 2 x 2 − 4 có đồ thị (C). Gọi h 1 là khoảng cách giữa hai điểm cực tiểu của (C) và h 2 là khoảng cách từ điểm cực đại của (C) tới trục hoành. Tỉ số h 1 h 2 là
A. 1 2 .
B. 5 4 .
C. 5 2 .
D. 4 5 .
Cho hàm số y = m x 3 − 3 m x 2 + 2 m + 1 x − m + 3 , đồ thị là C m và A 1 2 ; 4 . Gọi h là khoảng cách từ điểm A đến đường thẳng đi qua điểm cực đại, cực tiểu của C m . Giá trị lớn nhất của h bằng
A. 2 .
B. 2 2 .
C. 2 3 .
D. 3 .
Tìm số mệnh đề sai trong những mệnh đề sau
(1). Nếu hàm số f x đạt cực đại tại x0 thì x0 được gọi là điểm cực đại của hàm số.
(2). Giá trị cực đại (giá trị cực tiểu) của hàm số còn được gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
(3). Cho hàm số f x là hàm số bậc 3, nếu hàm số có cực trị thì đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt.
(4). Cho hàm số f x là hàm số bậc 3, nếu hàm số cắt trục Ox tại duy nhất một điểm thì hàm số không có cực trị.
A. 2
B. 3
C. 1
D. 4
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: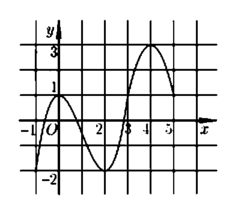
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y = f(x) xác định trên D = − 1 ; + ∞ \ 1 . Dưới đây là một phần đồ thị của y = f(x)
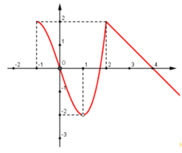
Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng:
(I) Số điểm cực đại của hàm số trên tập xác định là 1.
(II) Hàm số có cực tiểu là -2 tại x = 1
(III) Hàm số đạt cực đại tại x = 2
(IV) Hàm số đạt cực đại tại x = -1
A. 0
B. 1
C. 2
D. 3
Tìm tất cả các giá trị của tham số a để hàm số y = 2 x 3 + 9 a x 2 + 12 a 2 x + 1 có cực đại, cực tiểu và hoành độ điểm cực tiểu của đồ thị hàm số bằng 1.
A. a = − 1 2 .
B. a = − 1.
C. a = 1 2 .
D. a = 1.
Khoảng cách từ điểm cực tiểu của đồ thị hàm số y = x 3 − 3 x 2 + 2 đến trục tung bằng
A. 0.
B. 2.
C. 1.
D. 4