Đáp án C
Ta có y ' = 4 x 3 − 4 x = 4 x x 2 − 1 ⇒ y ' = 0 ⇔ x = 0 x = ± 1
Suy ra y 0 = 3 , y 1 = 2 , y 2 = 11 ⇒ m ax 0 ; 2 y = 11 , min 0 ; 2 y = 2 .
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hàm số y f(x) xác định trên
ℝ
và có đồ thị của hàm số
f
(
x
)
,
biết
f
(
3
)
+
f
(
2
)
f...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .
Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Cho bài toán: “Tìm Giá trị lớn nhất, giá tri nhỏ nhất của hàm số
y
f
(
x
)
x
+
1
x
-
1
trên
-
2
;
3
2
?”. Một học sinh giải như sau:Bước 1:
y
1
-
1
(
x...
Đọc tiếp
Cho bài toán: “Tìm Giá trị lớn nhất, giá tri nhỏ nhất của hàm số y = f ( x ) = x + 1 x - 1 trên - 2 ; 3 2 ?”. Một học sinh giải như sau:
Bước 1: y ' = 1 - 1 ( x - 1 ) 2 ∀ x ≢ 1
Bước 2: y ' = 0 ⇔ x = 2 ( L ) x = 0
Bước 3: f ( - 2 ) = - 7 3 ; f ( 0 ) = - 1 ; f 3 2 = 7 2 Vậy m a x [ - 2 ; 3 2 ] f ( x ) = 7 3 ; m i n [ - 2 ; 3 2 ] = - 7 3
Lời giải trên đúng hay sai ? Nêu sai thì sai lừ bưóc nào ?
A. Lời giải trên hoàn toàn đúng
B. Lời giải trên sai từ bước 1
C. Lời giải trên sai từ bước 2
D. Lời giải trên sai từ bước 3
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f(x), biết f(3)+f(20f(0)+f(1) và các khẳng định sau:1) Hàm số yf(x) có 2 điểm cực trị2) Hàm số yf(x) đồng biến trên khoảng
-
∞
;
0
3)
M
a
x
0
;
3
f...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là
A. 2
B. 3
C. 4
D. 5
Cho hàm số bậc 3:yf(x) có đồ thị như hình vẽ.Xét hàm số g(x)f[(x)]. Trong các mệnh đề dưới đây:g(x) đồng biến trên (-∞;0) và (2;+∞).Hàm số g(x) có bốn điểm cực trị.
m
a
x
-
1
;
1
g
x
0
.Phương trình g(x)0 có ba nghiệm.Số mệnh đề đúng là A. 3. B. 2. C. 1. D. 4.
Đọc tiếp
Cho hàm số bậc 3:y=f(x) có đồ thị như hình vẽ.
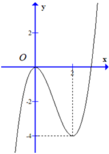
Xét hàm số g(x)=f[(x)]. Trong các mệnh đề dưới đây:
g(x) đồng biến trên (-∞;0) và (2;+∞).
Hàm số g(x) có bốn điểm cực trị.
m a x - 1 ; 1 g x = 0 .
Phương trình g(x)=0 có ba nghiệm.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 1.
D. 4.
Cho đồ thị yf’(x) trên [m;n] (như hình vẽ). Biết f(a) f(c)0; f(d)f(b)0 và
m
a
x
f
(
x
)
[
m
;
n
]
f
(
n
)
;
m
i
n...
Đọc tiếp
Cho đồ thị y=f’(x) trên [m;n] (như hình vẽ). Biết f(a)> f(c)>0; f(d)<f(b)<0 và
m
a
x
f
(
x
)
[
m
;
n
]
=
f
(
n
)
;
m
i
n
f
(
x
)
[
m
;
n
]
=
f
(
m
)
Số điểm cực trị của hàm số
y
=
f
(
x
)
trên [m;n] là
A. 6
B. 8
C. 9
D. 10
Cho hàm số
f
x
3
2
x
-
2
.
3
x
có đồ thị như hình vẽ sauCó bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Đường thẳng y 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
log
3
2
(2) Bất phương trình
f
x
≥
-...
Đọc tiếp
Cho hàm số f x = 3 2 x - 2 . 3 x có đồ thị như hình vẽ sau
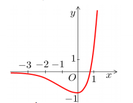
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là x = log 3 2
(2) Bất phương trình f x ≥ - 1 có nghiệm duy nhất.
(3) Bất phương trình f x ≥ 0 có tập nghiệm là - ∞ ; log 3 2
(4) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại 2 điểm phân biệt.
A. 2
B. 4
C. 1
D. 3
Cho hàm số
f
x
3
2
x
−
2.3
x
có đồ thị như hình vẽ sauCó bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Đường thẳng y0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
log
3
2
(2) Bất phương trình
f
x
≥...
Đọc tiếp
Cho hàm số f x = 3 2 x − 2.3 x có đồ thị như hình vẽ sau
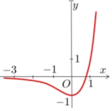
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y=0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
=
log
3
2
(2) Bất phương trình
f
x
≥
−
1
có nghiệm duy nhất.
(3) Bất phương trình
f
x
≥
0
có tập nghiệm là
−
∞
;
log
3
2
(4) Đường thẳng y=0 cát đồ thị hàm số (C) tại 2 điểm phân biệt
A. 2.
B. 4.
C. 1.
D. 3.
Cho các mệnh đề sau:1)
d
:
2
x
+
y
-
z
-
3
0
x
+
y
+
z
-
1...
Đọc tiếp
Cho các mệnh đề sau:
1) d : 2 x + y - z - 3 = 0 x + y + z - 1 = 0 phương trình tham số có dạng: x = 2 t y = 2 - 3 t z = t - 1
2) d : x + y - 1 = 0 4 y + z + 1 = 0 có phương trình chính tắc là d : x - 1 1 = y z = z + 1 4
3) Phương trình chính tắc của đường thẳng (d) đi qua điểm A(2,0,-3) và vuông góc với mặt phẳng P : 2 x - 3 y + 5 z - 4 = 0 là d : x - 2 2 = y - 3 = z + 3 5
Hỏi bao nhiêu mệnh đề đúng.
A.1
B. 3
C. 2
D. 0
Cho các mệnh đề:1. Nếu hàm số yf(x) liên tục trên
a
;
b
và
f
a
.
f
b
0
thì tồn tại
x
0
∈
a
;
b
sao cho
f
x
0
0.
2. Nếu hàm số...
Đọc tiếp
Cho các mệnh đề:
1. Nếu hàm số y=f(x) liên tục trên a ; b và f a . f b < 0 thì tồn tại x 0 ∈ a ; b sao cho f x 0 = 0.
2. Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm.
3. Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm duy nhất trên ( a ; b ) .
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai
B. Cả ba mệnh đề đều đúng
C. Cả ba mệnh đề đều sai
D. Có đúng một mệnh đề sai
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1