Đáp án A
Điểm M a ; b thuộc đồ thị (C)
=> b = a − 3 a + 1
⇒ a + b = a + a − 3 a + 1 = a + 4 a + 1 − 1 ≥ a + 1 + 4 a + 1 − 2 ≥ a + 1 + 4 a + 1 − 2 ≥ 4 − 2 = 2
Như vậy tổng khoảng cách từ M tới hai trục tọa độ nhỏ nhất bằng 2 ⇔ a = 1 b = − 1 ⇒ T = − 2
Đáp án A
Điểm M a ; b thuộc đồ thị (C)
=> b = a − 3 a + 1
⇒ a + b = a + a − 3 a + 1 = a + 4 a + 1 − 1 ≥ a + 1 + 4 a + 1 − 2 ≥ a + 1 + 4 a + 1 − 2 ≥ 4 − 2 = 2
Như vậy tổng khoảng cách từ M tới hai trục tọa độ nhỏ nhất bằng 2 ⇔ a = 1 b = − 1 ⇒ T = − 2
Cho hàm số y = x − 3 x + 1 C và điểm M( a;b) thuộc đồ thị (C). Đặt T = 3 a + b + 2 a b , khi đó để tổng khoảng cách từ điểm M đến hai trục toạ độ là nhỏ nhất thì mệnh đề nào sau đây là đúng?
A. − 3 < T < − 1
B. − 4 < T < − 3
C. − 1 < T < 1
D. − 3 < T < − 2
Cho hàm số y = x − 1 x + 1 có đồ thị (C), điểm M di động trên (C). Gọi d là tổng khoảng cách từ M đến hai trục tọa độ. Khi đó giá trị nhỏ nhất của d là
A. 207 250 .
B. 2 − 1.
C. 2 2 − 1.
D. 2 2 − 2.
Cho hàm số y=f(x) có đồ thị y=f'(x) cắt trục Ox hoành tại ba điểm có hoành độ -2<a<b như hình vẽ. Biết rằng f(-2)+f(1)=f(a)+f(b). Để hàm số y = f ( x + m ) có 7 điểm cực trị thì mệnh đề nào dưới đây là đúng
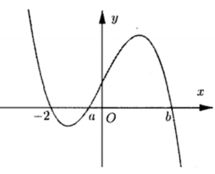
A. f(a)>0>f(-2)
B. f(-2)>0>f(a)
C. f(b)>0>f(a)
D. f(b)>0>f(-2)
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi M x M ; y M là điểm bất kỳ trên (D). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất thì tổng x M + y M bằng:
A. 2 2 - 1
B. 1
C. 2 - 2
D. 2 - 2 2
Cho hàm số y = x + 1 x - 1 có đồ thị là (C). Gọi M x M ; y M là một điểm bất kỳ trên (C). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất, tính tổng x M + y M
A. 2 - 2
B. 2 2 - 1
C. 1.
D. 2 - 2 2
Cho hàm số y = f(x) có đồ thị y = f’(x) cắt trục Ox tại 3 điểm có hoành độ a<b<c như hình vẽ. Mệnh đề nào dưới đây là đúng
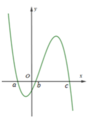
A. f(a)>f(b)>f(c)
B. f(c)>f(b)>f(a)
C. f(c)>f(a)>f(b)
D. f(b)>f(a)>f(c)
Cho hàm số y = 2 x + 1 x + 1 (C), gọi I là tâm đối xứng của đồ thị (C) và M(a;b) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị (C) tại điểm M cắt hai tiệm cận của đồ thị (C) lần lượt tại hai điểm A và B. Để tam giác IAB có bán kính đường tròn nội tiếp lớn nhất thì tổng a+b gần nhất với số nào sau đây?
A. -3.
B. 0.
C. 3.
D. 5.
Cho hàm số y = x + 1 x − 1 có đồ thị (C) và hai điểm M 0 ; 4 , N − 1 ; 2 . Gọi A;B là 2 điểm trên (C) sao cho các tiếp tuyến của (C) tại A và B song song đồng thời tổng khoảng cách từ M và từ N đến đường thẳng AB là lớn nhất. Tính độ dài đoạn thẳng AB
A. 5 6 3
B. 4 13 3
C. 2 5
D. 65
Xét đồ thị (C) của hàm số y = x 3 + 3 a x + b với a, b là các số thực. Gọi M, N là hai điểm phân biệt thuộc (C) sao cho tiếp tuyến với (C) tại hai điểm đó có hệ số góc bằng 3. Biết khoảng cách từ gốc tọa độ tới đường thẳng MN bằng 1, giá trị nhỏ nhất của a 2 + b 2 bằng
A. 3 2
B. 4 3
C. 6 5
D. 7 6