Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho hàm số
y
x
3
-
3
x
2
+
3
m
x
+
m
-
1
. Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục Ox có diện tích phần nằm phía trên trục Ox và phần nằm phía dưới trục Ox bằng nhau. Giá trị của m là A. 2/3. B. 4/5. C. 3/4. D. 3/5.
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 3 m x + m - 1 . Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục Ox có diện tích phần nằm phía trên trục Ox và phần nằm phía dưới trục Ox bằng nhau. Giá trị của m là
A. 2/3.
B. 4/5.
C. 3/4.
D. 3/5.
Cho hàm số
y
x
3
-
3
x
2
+
3
m
x
+
m
-
1
. Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục Ox có diện tích phần nằm phía trên trục Ox và phần nằm phía dưới trục Oxbằng nhau. Giá trị của m là A. 4/5 B. 3/4 C. 3/5 D. 2/3
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 3 m x + m - 1 . Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục Ox có diện tích phần nằm phía trên trục Ox và phần nằm phía dưới trục Oxbằng nhau. Giá trị của m là
A. 4/5
B. 3/4
C. 3/5
D. 2/3
Biết đồ thị hàm số
f
x
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S
1
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi
S
2
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết...
Đọc tiếp
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Cho đồ thị hàm số yf(x) đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox. A.
S
∫
−
3
4
f
x
d
x
B.
S
∫
−...
Đọc tiếp
Cho đồ thị hàm số y=f(x) đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox.
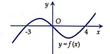
A. S = ∫ − 3 4 f x d x
B. S = ∫ − 3 0 f x d x + ∫ 0 4 f x d x
C. S = ∫ − 3 0 f x d x + ∫ 4 0 f x d x
D. S = ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
Hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
và trục hoành gồm hai phần, phần nằm phía trên trục hoành có diện tích
S
1
8
3
và phần nằm phía dưới trục hoành có diện tích
S
2
5
12
(tham khảo hình vẽ bên). Tính
I
∫
-...
Đọc tiếp
Hình phẳng giới hạn bởi đồ thị hàm số y = f x và trục hoành gồm hai phần, phần nằm phía trên trục hoành có diện tích S 1 = 8 3 và phần nằm phía dưới trục hoành có diện tích S 2 = 5 12 (tham khảo hình vẽ bên). Tính I = ∫ - 1 0 f 3 x + 1 dx

A. I = 27 4
B. I = 5 3
C. I = 3 4
D. I = 37 36
Cho hàm số
y
1
3
x
3
−
x
2
+
m
x
+
m
−
1
3
(m là tham số thực). Tìm m để hình phẳng giới hạn bởi đồ thị hàm số và trục Ox được chia thành hai phần có diện tích bằng nhau. A.
m
2
3
B. m 0 C. m 1 D.
m...
Đọc tiếp
Cho hàm số y = 1 3 x 3 − x 2 + m x + m − 1 3 (m là tham số thực). Tìm m để hình phẳng giới hạn bởi đồ thị hàm số và trục Ox được chia thành hai phần có diện tích bằng nhau.
A. m = 2 3
B. m = 0
C. m = 1
D. m = 1 2
Cho hàm số
y
x
2
-
m
x
(
0
m
4
)
có đồ thị (C). Gọi
S
1
là diện tích hình phẳng giới hạn bởi (C) và trục hoành;
S
2
là diện tích hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng xm,x4. Biết
S
1...
Đọc tiếp
Cho hàm số y = x 2 - m x ( 0 < m < 4 ) có đồ thị (C). Gọi S 1 là diện tích hình phẳng giới hạn bởi (C) và trục hoành; S 2 là diện tích hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x=m,x=4. Biết S 1 = S 2 , giá trị của m bằng
A. 10 3 .
B. 2.
C. 3.
D. 8 3 .
Hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
liên tục trên đoạn
[
1
;
3
]
,
trục Ox và hai đường thẳng
x
1
,
x
3
có diện tích là: A.
S
∫
1
3
f
x
d
x
B.
S
∫...
Đọc tiếp
Hình phẳng giới hạn bởi đồ thị hàm số y = f x liên tục trên đoạn [ 1 ; 3 ] , trục Ox và hai đường thẳng x = 1 , x = 3 có diện tích là:
A. S = ∫ 1 3 f x d x
B. S = ∫ 1 3 f x d x
C. S = ∫ 3 1 f x d x
D. S = ∫ 3 1 f x d x
Cho đồ thị hàm số
y
f
x
đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox. A.
S
∫
−
3
4
f
x
d
x
B.
S
∫
−...
Đọc tiếp
Cho đồ thị hàm số y = f x đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox.
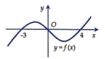
A. S = ∫ − 3 4 f x d x
B. S = ∫ − 3 0 f x d x + ∫ 0 4 f x d x
C. S = ∫ − 3 0 f x d x + ∫ 4 0 f x d x
D. S = ∫ 0 − 3 f x d x + ∫ 0 4 f x d x




