Đáp án B.
Tập xác định: D = ℝ \ − 1 .
Hàm số phân thức bậc nhất trên bậc nhất không thể đồng biến (hay nghịch biến) trên R và hàm số không có cực trị. Loại A, C, D.
Đáp án B.
Tập xác định: D = ℝ \ − 1 .
Hàm số phân thức bậc nhất trên bậc nhất không thể đồng biến (hay nghịch biến) trên R và hàm số không có cực trị. Loại A, C, D.
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số y = log 2 x 2 - 2 x - 3 . Xét các khẳng định sau
(I) Hàm số đồng biến trên R
(II) Hàm số đồng biến trên khoảng 3 ; + ∞
(III) Hàm số nghịch biến trên khoảng - ∞ ; - 1
Trong các khẳng định (I), (II) và (III) có bao nhiêu khẳng định đúng
A. 1
B. 2
C. 0
D. 3
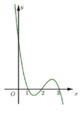
Cho hàm số f(x) xác định trên R và hàm số y = f’(x) có đồ thị như hình bên dưới:
Xét các khẳng định sau:
(I) Hàm số y = f(x) có ba cực trị.
(II) Phương trình f(x) = m + 2018 có nhiều nhất ba nghiệm.
(III) Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
Số khẳng định đúng là:
A. 1
B. 2
C. 0
D. 3
Cho hàm số y = x 2 3 + 2017 , có các khẳng định sau.
I. Hàm số luôn đồng biến trên − ∞ ; + ∞
II. Hàm số có một điểm cực tiểu là x = 0
III. Giá trị lớn nhất bằng 2017.
IV. Hàm số luôn nghịch biến trên − ∞ ; + ∞
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Cho các khẳng định:
(I): Hàm số y=2 đồng biến trên ℝ .
(II): Hàm số y = x 3 - 12 x nghịch biến trên khoảng (-1;2).
(III): Hàm số y = 2 x - 5 x - 2 đồng biến trên các khoảng - ∞ ; 2 và 2 ; + ∞
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
A. 0.
B. 2.
C. 3.
D. 1.
Cho hàm số y = f(x) xác định trên
ℝ
và có đồ thị hàm số y = f '(x) như hình vẽ bên.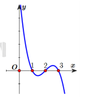 Xét các khẳng định sau:
Xét các khẳng định sau:
(I) Hàm số y = f(x) có ba cực trị.
(II) Phương trình f(x) = m + 2018 có nhiều nhất ba nghiệm.
(III) Hàm số y = f(x + 1) nghịch biến trên khoảng (0;1) .
Số khẳng định đúng là:
A. 1
B. 3
C. 2
D. 0
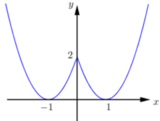
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình dưới đây:
Xét các mệnh đề sau:
(I). Hàm số nghịch biến trên khoảng (0;1)
(II). Hàm số đồng biến trên khoảng (-1;2)
(III). Hàm số có ba điểm cực trị
(IV). Hàm số có giá trị lớn nhất bằng 2.
Số mệnh đề đúng trong các mệnh đề trên là:
A. 4
B. 2
C. 3
D. 1
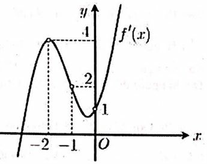
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số y = x - 2 x - 1 . Xét các mệnh đề sau:
1. Hàm số đã cho đồng biến trên - ∞ ; 1 ∪ 1 ; + ∞ .
2. Hàm số đã cho đồng biến trên ℝ \ { 1 } .
3. Hàm số đã cho đồng biến trên từng khoảng xác định.
4. Hàm số đã cho đồng biến trên các khoảng - ∞ ; - 1 và - 1 ; + ∞ .
Số mệnh đề đúng là:
A. 3
B. 2
C. 1
D. 4