Question

Cho hàm số y= - x 2  (P) và đường thẳng (d): y = 2mx - 5

b) Chứng tỏ rằng trên mặt phẳng Oxy đường thẳng (d) và parabol (P) luôn cắt nhau tại hai điểm phân biệt. Tìm tọa độ hai giao khi m = 2.

Answer 1

b) Phương trình hoành độ giao điểm của (P) và (d) là:

- x 2  = 2mx - 5 ⇔  x 2  + 2mx - 5 = 0

Δ'= m 2 + 5 > 0 với ∀m ∈ R

Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.

Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:

- x 2 = 4x - 5 ⇔ x 2  + 4x - 5 = 0

Δ = 4 2  - 4.1.(-5) = 36

⇒ Phương trình có 2 nghiệm

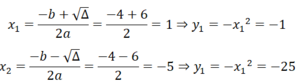
Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)