Với m > 1 thì hàm số đã cho không bị suy biến.
y = m là tiệm cận ngang, x = m là tiệm cận đứng của đồ thị hàm số. Vậy giao điểm hai tiệm cận là I(m;m).
Ta có: y 1 = x 1 nên điểm I thuộc đường thẳng có phương trình y = x.
Chọn A
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D=R\{3}.
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị.
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. 1,2,3.
B. 3,4.
C. 2,3,4.
D. 1,4.
Cho các mệnh đề sau
(1) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → x 0 f x = y 0 h o ặ c lim x → x 0 f x = y 0
(2) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → - ∞ f x = y 0 h o ặ c lim x → + ∞ f x = y 0
(3) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = + ∞ h o ặ c lim x → x 0 - f x = - ∞
(4) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = - ∞ h o ặ c lim x → x 0 - f x = - ∞
Trong các mệnh đề trên, số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. 4
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7
Cho hàm số y = m x + 1 x - 2 m với tham số m ≠ 0 Giao điểm của hai đường tiệm cận của đồ thị hàm số thuộc đường thẳng có phương trình nào dưới đây?
A. 2x+y=0
B. y=2x
C. x-2y=0
D. x+2y=0
Cho hàm số y = m x + 1 x - 2 m với tham số m ≠ 0 . Giao điểm của hai đường tiệm cận của đồ thị hàm số thuộc đường thẳng có phương trình nào dưới đây?
Cho hàm số y= (2x-1)/( x+1) có đồ thị (C). Gọi M là một điểm bất kì trên (C) . Tiếp tuyến của (C) tại M cắt các đường tiệm cận của (C) tại A và B. Gọi I là giao điểm của các đường tiệm cận của (C). Tình diện tích của tam giác IAB
Cho hàm số y = x + 2 1 - x 2 . Xét các mệnh đề sau đây:
(I). Hàm số có tập xác định D=(-1;1).
(II). Đồ thị hàm số có 2 đường tiệm cận ngang là y=1 và y=-1.
(III). Đồ thị hàm số có 2 đường tiệm cận đứng là x=1 và x=-1.
(IV). Hàm số có một cực trị.
Số mệnh đề đúng là:
A.3
B.1
C.2
D.4
Tìm các giá trị của tham số m để đồ thị hàm số: y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 m ( 1 - 2 m ) x có điểm cực đại và điểm cực tiểu nằm trên đường thẳng có phương trình: y = - 4 x ( d )
A. m ∈ 1
B. m ∈ 0 ; 1
C. m ∈ 0 ; 1 2 ; 1
D. m ∈ 1 2
Với giá trị nào của m, đồ thị hàm số y = x + 1 - x 2 + 3 x x 2 + ( m + 1 ) x - m - 2 có đúng hai đường tiệm cận?
A. m ≤ - 2 m ≠ - 3
B.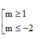 
C. mọi m
D. 
