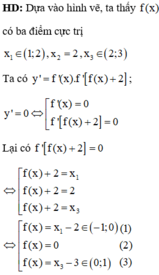
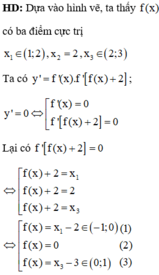
Dựa vào hình vẽ, ta thấy (1) có 3 nghiệm phân biệt; (2) có 2 nghiệm phân biệt; (3) có 3 nghiệm phân biệt và các nghiệm trên đều là nghiệm đơn hoặc bội lẻ
Vậy hàm số đã cho có 3 + 3 + 2 + 3 = 11 điểm cực trị. Chọn B
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi hàm số y = f f x + 2 có bao nhiêu điểm cực trị?
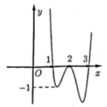
A. 10
B. 11
C. 12
D. 9
Cho hàm số y = f(x) liên tục trên R, hàm số y = f'(x) có đồ thị như hình vẽ bên. Hỏi hàm số y = 2 f x − x 2 + 2 x + 2018 có bao nhiêu điểm cực trị?
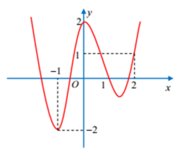
A. 1
B. 2
C. 3
D. 4
Cho hàm số y=f(x) liên tục trên R và có đồ thị hàm số như hình vẽ dưới. Hỏi hàm số đó có bao nhiêu điểm cực trị?
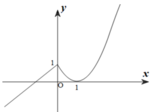
A. 0
B. 3
C. 1
D. 2
Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y = f'(x) như hình vẽ. Hàm số y = f ( 2 x 2 + x ) có bao nhiêu cực trị?
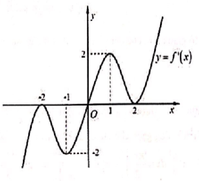
A. 4.
B. 5.
C. 3.
D. 1.
Cho hàm số y=f(x) liên tục trên R. Hàm số y=f'(x) có đồ thị như hình bên. Hỏi hàm số
y
=
f
(
x
)
+
2017
-
2019
x
2018
có bao nhiêu điểm cực trị
A. 4
B. 3
C. 2
D. 1
Cho hàm số y=f(x) xác định và liên tục trên R, có đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hàm số g(x)=f(x) – 1/2 x2+ x-8 có bao nhiêu điểm cực tiểu?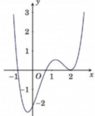
A. 3
B. 2
C. 1.
D. 4
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
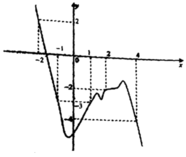
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Cho hàm số y=f(x) có đạo hám liên tục trên R và có đồ thị f '(x) như hình vẽ bên. Biết rằng f - 3 > 8 , f 2 < 1 2 , f 4 > 9 2 Số điểm cực trị của hàm số y = f ( x ) - x - 1 2 2 là
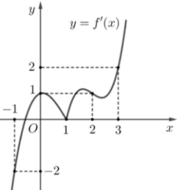
A. 7
B. 5
C. 8
D. 6
Cho hàm số y = f(x) liên tục trên R có đồ thị y = f'(x) như hình vẽ bên. Biết f 1 = 0 . Xác định số điểm cực trị của đồ thị hàm số y = |f(x)|.
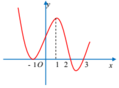
A. 5
B. 6
C. 4
D. 3
