Đáp án A
Phương pháp:
Tính y’, giải bất phương trình y’>0
Cách giải:
![]()
Với
![]()
![]()
Đáp án A

Phương pháp:
Tính y’, giải bất phương trình y’>0
Cách giải:
![]()
Với
![]()
![]()
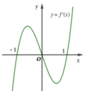
Cho hàm số y=f(x) Hàm số y=f'(x) có đồ thị như hình bên
Hàm số y=f(1-3x) đồng biến trên khoảng
A. (1;2)
B . 2 ; + ∞
C . 0 ; 1 3
D . - 1 3 ; 0
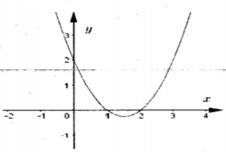
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng nào dưới đây?
A. ( 3 ; + ∞ )
B. ( - 3 ; - 1 )
C. ( 1 ; 3 )
D. (0;1)
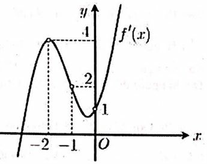
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
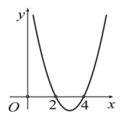
Cho hàm số y=f(x) có đồ thị hàm số y=f’(x) như hình bên dưới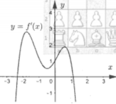
Hàm số g(x)=f(1-4x) đồng biến trên khoảng nào trong các khoảng sau?
![]()
![]()
![]()
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: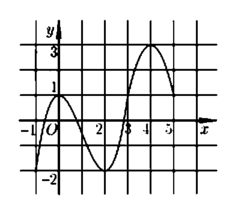
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ bên dưới. Hàm số y = f 3 − x 2 đồng biến trên khoảng
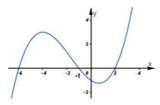
A. (2;3)
B. (-2;-1)
C. (0;1)
D. (-1;0)
Cho hàm số y = f(x) Biết hàm số y = f '(x) có đồ thị như hình vẽ bên dưới. Hàm số y = f 3 − x 2 đồng biến trên khoảng:
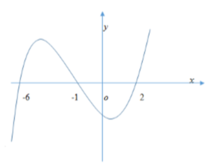
A. (0;1)
B. (-1;0)
C. (2;3)
D. (-2;-1)
Cho hàm số y = f(x). Biết hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Hàm số y = 3 - x 2 đồng biến trên khoảng
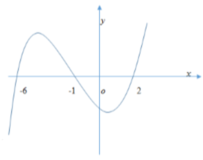
A. (0;1)
B. (-1;0)
C. (2;3)
D. (-2;-1)
Cho hàm số f(x) có đồ thị hàm số y = f’(x) được cho như hình vẽ bên. Hàm số y = f cos x + x 2 - x đồng biến trên khoảng
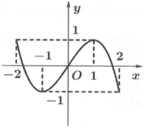
A. (1;2)
B. (-1;0)
C. (0;1)
D. (-2;-1)