Các câu hỏi tương tự
Cho hàm số y f(x). Hàm số y f (x) có bảng biến thiên như hình vẽ:Bất phương trình
e
x
≥
m
-
f
(
x
)
có nghiệm
x
∈
4
;
16
khi và chỉ khi A.
m
≤
f
(
4
)
+
e...
Đọc tiếp
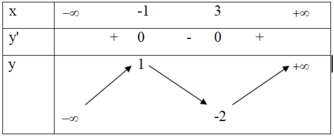
Cho hàm số y = f(x). Hàm số y = f '(x) có bảng biến thiên như hình vẽ:
Bất phương trình e x ≥ m - f ( x ) có nghiệm x ∈ 4 ; 16 khi và chỉ khi
A. m ≤ f ( 4 ) + e 2
B. m < f ( 4 ) + e 2
C. m ≤ f ( 16 ) + e 4
D. m < f ( 16 ) + e 4
Cho hàm số yf(x) Hàm số yf (x) có bảng biến thiên như sauBất phương trình
m
+
e
f
(
x
)
e
x
có nghiệm
x
∈
-
1
;
1
khi và chỉ khi A.
m
1
e
-...
Đọc tiếp
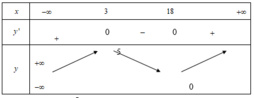
Cho hàm số y=f(x) Hàm số y=f '(x) có bảng biến thiên như sau
Bất phương trình m + e f ( x ) < e x có nghiệm x ∈ - 1 ; 1 khi và chỉ khi
A. m < 1 e - e f ( - 1 )
B. m ≤ 1 e - e f ( 1 )
C. m ≤ 1 e - e f ( - 1 )
D. m < e - e f ( 1 )
Cho hàm số yf(x) có đạo hàm đến cấp hai trên R. Bảng biến thiên của hàm số yf(x) như hình vẽ. Bất phương trình
m
+
x
2
≤
f
x
+
1
3
x
3
nghiệm đúng với mọi x ∈(0;3) khi và chỉ khi A. m f (0). B. m≤ f (3). C. m≤ f (0). D. m f (1)−
2
3
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm đến cấp hai trên R. Bảng biến thiên của hàm số y=f'(x) như hình vẽ. Bất phương trình m + x 2 ≤ f x + 1 3 x 3 nghiệm đúng với mọi x ∈(0;3) khi và chỉ khi
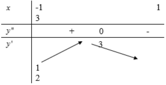
A. m< f (0).
B. m≤ f (3).
C. m≤ f (0).
D. m< f (1)− 2 3
Cho hàm số yf(x) có bảng biến thiên như sau:Bất phương trình
f
x
3
e
x
+
2
+
m
có nghiệm
x
∈
-
2
;
2
khi và chỉ khi: A.
m
≥
f
-
2...
Đọc tiếp
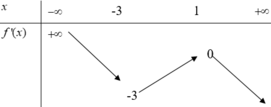
Cho hàm số y=f(x) có bảng biến thiên như sau:
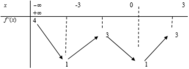
Bất phương trình f x < 3 e x + 2 + m có nghiệm x ∈ - 2 ; 2 khi và chỉ khi:
A. m ≥ f - 2 - 3
B. m > f 2 - 3 e 4
C. m ≥ f 2 - 3 e 4
D. m ≥ f - 2 - 3
Cho hàm số yf(x) có bảng biến thiên như hình vẽ, biết f(-1)f(2) và f(0)f(3)Phương trình f(2sinx+1)f(m) có đúng ba nghiệm thuộc đoạn
-
π
2
;
π
2
khi và chỉ khi A.
m
∈
0
;
2
B.
m
∈
1...
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, biết f(-1)=f(2) và f(0)=f(3)
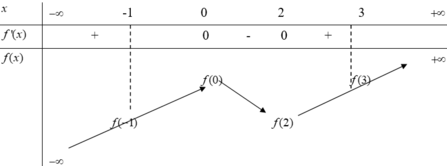
Phương trình f(2sinx+1)=f(m) có đúng ba nghiệm thuộc đoạn - π 2 ; π 2 khi và chỉ khi
A. m ∈ 0 ; 2
B. m ∈ 1 ; 3 \ 0 ; 2
C. m ∈ f ( 2 ) ; f ( 0 )
D. m ∈ - 1 ; 3
Cho hàm số yf(x). Hàm số yf (x) có bảng biến thiên như sauBất phương trình
f
(
e
x
)
e
2
x
+
m
nghiệm đúng với mọi
x
∈
(
ln
2
;
ln
4
)
khi và chỉ khi A.
m
≥
f
(
2
)
-
4
B. ...
Đọc tiếp
Cho hàm số y=f(x). Hàm số y=f' (x) có bảng biến thiên như sau

Bất phương trình f ( e x ) < e 2 x + m nghiệm đúng với mọi x ∈ ( ln 2 ; ln 4 ) khi và chỉ khi
A. m ≥ f ( 2 ) - 4
B. m ≥ f ( 4 ) - 16
C. m > f ( 2 ) - 4
D. m > f ( 4 ) - 16
Cho hàm số yf(x). Hàm số yf(x) có bảng biến thiên như sauBất phương trình
f
e
x
e
x
+
m
nghiệm đúng với mọi
x
∈
-
1
;
1
khi và chỉ khi A.
m
≥
f...
Đọc tiếp
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng biến thiên như sau

Bất phương trình f e x < e x + m nghiệm đúng với mọi x ∈ - 1 ; 1 khi và chỉ khi
A. m ≥ f 1 e - 1 e
B. m > f - 1 - 1 e
C. m ≥ f - 1 - 1 e
D. m > f 1 e - 1 e
Cho hàm số y f(x) có đạo hàm trên các khoảng (-1;0); (0;5) và có bảng biến thiên như hình bên. Phương trình f(x) m có nghiệm duy nhất trên (-1;0)
∪
(0;5) khi và chỉ khi m thuộc tập hợp A.
(
4
+
2
5
;
10
)
B.
-...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên các khoảng (-1;0); (0;5) và có bảng biến thiên như hình bên. Phương trình f(x) = m có nghiệm duy nhất trên (-1;0) ∪ (0;5) khi và chỉ khi m thuộc tập hợp
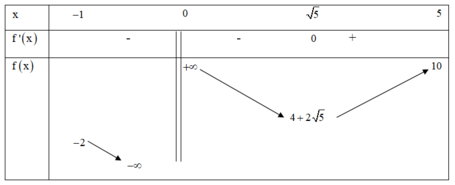
A. ( 4 + 2 5 ; 10 )
B. - ∞ ; - 2 ∪ { 4 + 2 5 } ∪ [ 10 + ∞ )
C. - ∞ ; - 2 ∪ [ 4 + 2 5 ; + ∞ )
D. - ∞ ; - 2 ∪ [ 10 + ∞ )
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
có bảng biến thiên như sauKhi đó
|
f
(
x
)
|
m
có bốn nghiệm phân biệt
x
1
x
2...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có bảng biến thiên như sau
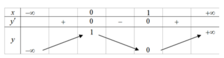
Khi đó | f ( x ) | = m có bốn nghiệm phân biệt x 1 < x 2 < x 3 < 1 2 < x 4 khi và chỉ khi
A. 0 < m ≤ 1
B. 1 2 < m < 1
C. 1 2 ≤ m < 1
D. 0 < m < 1