Ta có:
.
Số nghiệm của phương trình f x = m và số giao điểm của đồ thị hàm số y = f x và đường thẳng y = m song song với trục hoành.
Do đó để phương trình * có 4 nghiệm phân biệt thì 1 < m < 2 .
Chọn C.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau.
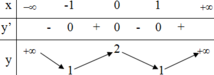
Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-m=0 có 4 nghiệm phân biệt.
A. m ϵ (1 ;2]
B. m ϵ [1 ;2)
C. m ϵ (1 ;2)
D. m ϵ[1 ;2)
Cho hàm số y = f(x) có bảng biến thiên như sau:
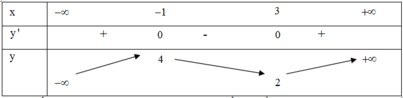
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m + 1 có 3 nghiệm thực phân biệt?
A. –3 ≤ m ≤ 3
B. –2 ≤ m ≤ 4
C. –2 < m < 4
D. –3 < m < 3
Cho hàm số y=f(x) có bảng biến thiên như sau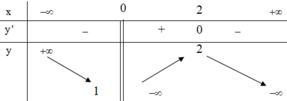
Tập hợp tất cả các giá trị của tham số m để phương trình f(x)+m=0 có 2 nghiệm phân biệt là
A. (-2;1)
B. [-1;2)
C. (-1;2)
D. (-2;1]
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c , d ∈ ℝ ) có bảng biến thiên như hình sau:
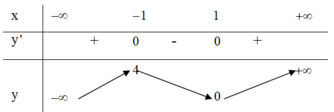
Tìm tất cả giá trị thực của tham số m để phương trình m = f ( x ) có 4 nghiệm phân biệt trong đó có đúng một nghiệm dương.
A.m > 2
B.0 < m < 4
C.m > 0
D.2 < m < 4
Cho hàm số y = f(x) có bảng biến thiên như sau:
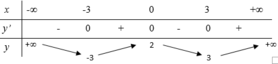
Tìm tất cả giá trị thực của tham số m để phương trình f(x) - m - 0 có bốn nghiệm phân biệt.
A. - 3 < m < 2
B. - 3 ≤ m ≤ 2
C. m < - 2
D. m > - 3
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1=m có đúng 2 nghiệm
A. -2 < m < -1
B. m > 0, m = -1
C. m = -2, m > -1
D. m = -2, m ≥ -1
Cho hàm số y=f(x) xác định trên ℝ \ 2 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau.
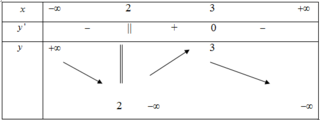
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm phân biệt.
A. m ∈ 2 ; 3
B. m ∈ 2 ; 3
C. m ∈ 2 ; 3
D. m ∈ 2 ; 3
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như hình vẽ. Tìm tất cả các giá trị thực của m để phương trình 1 2 f x - m = 0 có đúng hai nghiệm phân biệt.
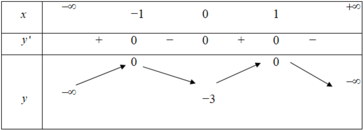
A. m = 0 m < - 3 2
B. m < - 3
C. m < - 3 2
D. m = 0 m < - 3
Cho hàm số y=f(x) xác định trên ℝ \ 1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ.
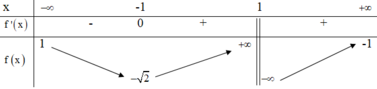
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f x = m có ba nghiệm thực phân biệt.
A. − 2 ; − 1 .
B. − 2 ; − 1 .
C. − 1 ; 1 .
D. − 1 ; 1 .
Cho hàm số y = f(x) có bảng biến thiên dưới đây.
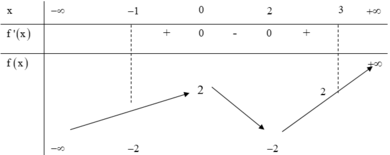
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = f(m) có ba nghiệm phân biệt
A. m ∈ - 2 ; 2
B. m ∈ - 1 ; 3 \ 0 ; 2
C. m ∈ - 1 ; 3
D. m ∈ - 1 ; 3 \ 0 ; 2
