Các câu hỏi tương tự
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
v
ớ
i
a
,
b
,
c
,
d
∈
ℝ
,
a...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho hai hàm số
f
(
x
)
x
4
-
m
-
1
x
2
+
2
và
g
(
x
)
2
x
4
-
4
x...
Đọc tiếp
Cho hai hàm số f ( x ) = x 4 - m - 1 x 2 + 2 và g ( x ) = 2 x 4 - 4 x 2 + 3 m . Giả sử đồ thị hàm số f(x) có ba điểm cực trị là A, B, C và đồ thị hàm số g(x) có ba điểm cực trị là M, N, P. Có bao nhiêu giá trị của tham số m để hai tam giác ABC và MNP đồng dạng với nhau?
A. 1.
B. 0.
C. 2.
D. 3.
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số y f( x) ax4+ bx2+ c ( a 0) có đồ thị (C), đồ thị hàm số y f’(x). Đồ thị hàm số y f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành? A.
7
15
B.
8
15
C.
14
15
D.
16
15
Đọc tiếp
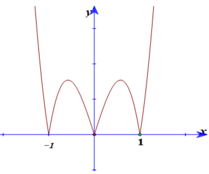
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 7 15
B. 8 15
C. 14 15
D. 16 15
Cho hàm số yf(x)
a
x
3
+
b
x
2
+
c
x
+
d
,
(
a
,
b
,
c
,
d
∈
R
,
a khác 0) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y 4 tại điểm có hoành độ âm và đồ thị của hàm số y...
Đọc tiếp
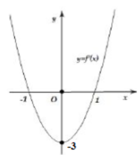
Cho hàm số y=f(x)= a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ R , a khác 0) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y= f ' ( x ) cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giời hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox
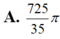
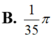
![]()
![]()
Cho hai hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
-
1
2
và
g
(
x
)
d
x
2
+
e
x
+
1
(
a
,
b
,
c
,
d...
Đọc tiếp
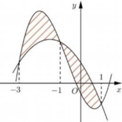
Cho hai hàm số f ( x ) = a x 3 + b x 2 + c x - 1 2 và g ( x ) = d x 2 + e x + 1 ( a , b , c , d , e ∈ ℝ ) . Biết rằng đồ thị của hàm số y = f(x) và y = g(x) cắt nhau tại ba điểm có hoành độ lần lượt là –3; –1;1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
A. 9 2
B. 8
C. 4
D. 5
Cho hàm số
f
(
x
)
x
3
+
3
a
x
2
+
3
x
+
3
có đồ thị (C) và
g
(
x
)
x
3
+
3
b
x
2
+
9
x
+
5
có đồ thị (H), với a, b lá các tham số t...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + 3 a x 2 + 3 x + 3 có đồ thị (C) và g ( x ) = x 3 + 3 b x 2 + 9 x + 5 có đồ thị (H), với a, b lá các tham số thực. Đồ thị (C), (H) có chung ít nhất 1 điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức P = a + 2 b
A. 21
B. 2 6 + 6.
C. 3 + 5 3 .
D. 2 6 .
Tìm khẳng định đúng trong các khẳng định sau đây:A. Hàm số y
x
3
- 5 có hai cực trị;B. Hàm số y
x
4
/4 + 3
x
2
- 5 luôn đồng biến;C. Tiệm cận ngang của đồ thị hàm số
y
3
x
-...
Đọc tiếp
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7