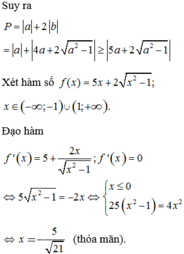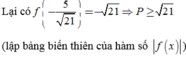Các câu hỏi tương tự
Cho hàm số
f
(
x
)
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3...
Đọc tiếp
Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
,
với m là tham số thực.
Hàm số
g
(
x
)
=
x
2
+
4
x
+
5
x
+
2
có đồ thị C và bảng biến thiên sau:
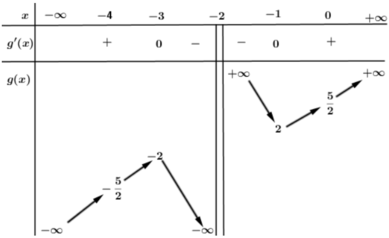
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1
A. m> 2
B. 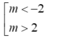
C. m < -5/2
D. m> 5 2
Cho hai hàm số
f
(
x
)
x
4
-
m
-
1
x
2
+
2
và
g
(
x
)
2
x
4
-
4
x...
Đọc tiếp
Cho hai hàm số f ( x ) = x 4 - m - 1 x 2 + 2 và g ( x ) = 2 x 4 - 4 x 2 + 3 m . Giả sử đồ thị hàm số f(x) có ba điểm cực trị là A, B, C và đồ thị hàm số g(x) có ba điểm cực trị là M, N, P. Có bao nhiêu giá trị của tham số m để hai tam giác ABC và MNP đồng dạng với nhau?
A. 1.
B. 0.
C. 2.
D. 3.
Cho hàm số y f(x) có đồ thị như hình vẽ bên dưới . Để đồ thị hàm số h(x)
|
f
2
(
x
)
+
f
(
x
)
+
m
|
có số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số
m
m
o
. Tìm mệnh đề đúng trong các mệnh đề sau:
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới . Để đồ thị hàm số h(x) = | f 2 ( x ) + f ( x ) + m | có số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số m = m o . Tìm mệnh đề đúng trong các mệnh đề sau:
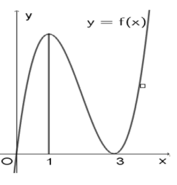
![]()
![]()
![]()
![]()
Cho hàm số y f(x) có đồ thị như hình vẽ bên dưới . Để đồ thị hàm số h(x)
f
2
(
x
)
+
f
(
x
)
+
m
có số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số
m
m
o
Tìm mệnh đề đú...
Đọc tiếp
Cho hàm số y= f(x) có đồ thị như hình vẽ bên dưới . Để đồ thị hàm số h(x) = f 2 ( x ) + f ( x ) + m có số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số m = m o
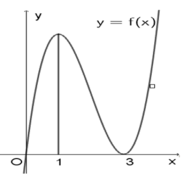
Tìm mệnh đề đúng trong các mệnh đề sau
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số
f
(
x
)
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
với là tham số thực. Hàm số có đồ thị (C) và bảng biến thiên sau: Tìm sao...
Đọc tiếp
Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
với ![]() là tham số thực. Hàm số
là tham số thực. Hàm số ![]() có đồ thị (C) và bảng biến thiên sau:
có đồ thị (C) và bảng biến thiên sau:
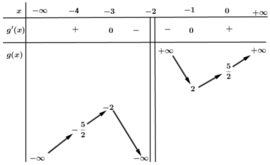
Tìm ![]() sao cho hàm số
sao cho hàm số ![]() đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn - 1
đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn - 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Biết hai hàm số
f
(
x
)
x
3
+
a
x
2
+
4
x
-
2
và
g
(
x
)
-
x
3
+
b
x
2
-
2
x...
Đọc tiếp
Biết hai hàm số f ( x ) = x 3 + a x 2 + 4 x - 2 và g ( x ) = - x 3 + b x 2 - 2 x + 3 có chung ít nhất một điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức P = a + b
A. 3 2
B. 6 2
C. 6
D. 3
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
2
x
3
-
3
(
m
+
1
)
x
2
+
6
m
x
có hai điểm cực trị...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị A , B sao cho đường thẳng AB vuông góc với đường thẳng : y = x + 2 .

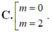
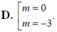
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y2x3-3( m+1) x2+ 6mx có hai điểm cực trị A; B sao cho đường thẳng AB vuông góc với đường thẳng y x+ 2. A. 0; 3 B. 2; 4 C. 0; 2 D. 1; 3
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2x3-3( m+1) x2+ 6mx có hai điểm cực trị A; B sao cho đường thẳng AB vuông góc với đường thẳng y= x+ 2.
A. 0; 3
B. 2; 4
C. 0; 2
D. 1; 3