a) 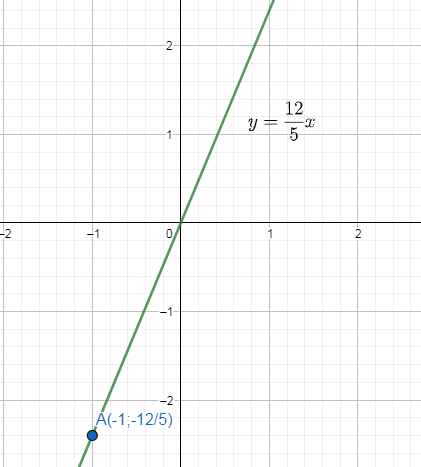
b) Trong các điểm trên, không có điểm nào thuộc đồ thị hàm số.
a) 
b) Trong các điểm trên, không có điểm nào thuộc đồ thị hàm số.
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị là \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
1) Cho hàm số bậc nhất y = (2m -1)x-4 có đồ thị là đường thẳng (d) \(\left(m\ne\dfrac{1}{2}\right)\)
a) Vẽ đồ thị hàm số
b) Tìm tọa độ giao điểm C của (d) với đồ thị hàm số \(y=3x+2\left(d_1\right)\)
2) Tìm m để (d) cắt trục Ox , Oy lần lượt tại A , B sao cho tam giác AOB cân
Cho hàm số \(y=\left(m-1\right)x^2\) \(\left(m\ne1\right)\) có đồ thị là parabol (P)
a, Xác định m để (P) đi qua điểm \(A\left(-\sqrt{3};1\right)\)
b, Với giá tị m vừa tìm được ở trên, hãy;
i, Vẽ (P) trên mặt phẳng tọa độ
ii, Trong các điểm A(1;1), B\(\left(-1;\dfrac{1}{3}\right)\) và C(15;-75), điểm nào thuộc (P), điểm nào không thuộc (P) ?
iii, Tìm các điểm trên (P) có hoành độ bằng 1
iv, Tìm các điểm trên (P) có tung độ gấp đôi hoành độ
Bài 1:
a) Vẽ đồ thị (d) của hàm số y = -2x + 3
b) Xác định các hệ số a và b của hàm số (d'): y = ax + b, biết đường thẳng (d') song song (d) và cắt trục hoành tại điểm có hoành độ bằng 2.
Bài 2: Rút gọn
C =\(1\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}\:\left(a>0,\:b>0\right)\)
Cho hàm số \(y=mx+1\left(m\ne0\right)\left(1\right)\)
1) Tìm m để đồ thị hàm số (1) đi qua điểm \(M\left(-1;-1\right)\). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
2) Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng \(y=\left(m^2-2\right)x+2m+3\)
3) Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng \(\dfrac{2}{\sqrt{5}}\).
1. cho hàm số \(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)\left(d^2+1\right)\ge2017\) có đồ thị (P). Xác định a, b để đường thẳng (d) : y = ax + b cắt trục tung tại điểm có hoành độ bằng -2 và cắt đồ thị (P) tại điểm có hoành độ bằng 2.
2. cho PT: \(x^2-2\left(m+2\right)x+\left(m^2+4m-12\right)=0\) (m là tham số). Tìm m để PT có nghiệm \(x_1;x_2\) thỏa mãn \(\left|x_1+x_2\right|\le6\)
Bài 1: Giải phương trình
a) \(\sqrt{x^2+4x+4}=2\)
b) \(\sqrt{4x-8}-7\sqrt{\dfrac{x-2}{49}}=5\)
Bài 2: Trong mặt phẳng tọa độ Oxy:
a) Vẽ đồ thị (d₁) của hàm số y = \(-\dfrac{1}{2}x+\dfrac{3}{2}\)
b) Gọi A và B là giao điểm của đồ thị (d₁) với các trục tọa độ. Tính diện tích ∆OAB (với O là gốc tọa độ)
Bài 3: Rút gọn
A= \(\dfrac{2\sqrt{x}-4}{3\sqrt{x}-4}+\dfrac{x+22\sqrt{x}-32}{3x-10\sqrt{x}+8}+\dfrac{4+2\sqrt{x}}{\sqrt{x}-2}\:\left(x\:\ge0;\:x\ne4;\:x\ne\dfrac{16}{9}\right)\)
Câu 1: Cho hàm số y= \(f\left(x\right)=x^2+2x-1\)
a. Tính các giá trị \(f\left(-1\right),\) \(f\left(0\right)\) và \(f\left(1\right)\)
b. Tìm toạ độ các điểm có tung độ bằng -1 trên đồ thị hàm số
Cho hàm số \(y=\left(m-1\right)x+26.\text{Hãy xác định m để}\)
a. Hàm số trên đồng biến
b. Đồ thị của hàm số đi qua điểm \(\text{A (1;-2) }\).Vẽ đồ thị hàm số vừa tìm được
c. Đồ thị của hàm số đã cho song song với đồ thị hàm số \(y=\left(4023-m\right)x-11\)