Đáp án A
Đồ thị hàm số y = 2 x + 1 x − 1 C có M 1 ; 2 là giao điểm của 2 tiệm cận
Không có tiếp tuyến nào của (C) đi qua.
Đáp án A
Đồ thị hàm số y = 2 x + 1 x − 1 C có M 1 ; 2 là giao điểm của 2 tiệm cận
Không có tiếp tuyến nào của (C) đi qua.
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0, x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ)
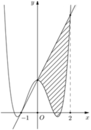
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số y = x 3 - 3 x 2 + m x - m + 1 có đồ thị (C) và điểm A(0;2) Gọi S là tập họp tất cả các giá trị nguyên của m để có ít nhất 2 tiếp tuyến của đồ thị (C) đi qua A . Tìm số phần tử của S.
A. 2
B. 3
C. 0.
D. 1.
Cho đồ thị (C) của hàm số y = x 3 - 3 x + 2 . Số các tiếp tuyến với đồ thị (C) mà các tiếp tuyến đó vuông góc với đường thẳng d : y = - 1 3 x + 1 là
A. 1
B. 2
C. 3
D. 0
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số y = x + 2 x + 1 có đồ thị (C). Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị (C) với trục tung là
A. y = x – 2
B. y = –x + 2
C. y = –x + 1
D. y = –x –2
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 có đồ thị là (C). Gọi T là tập hợp tất cả các điểm thuộc đường thẳng y=x-1 mà từ điểm đó kẻ được đúng 2 tiếp tuyến đến đồ thị (C). Tìm tổng tung độ của các điểm thuộc T.
A. ‒1
B. 0
C. 1
D. 2